Idee

Die Binomialverteilung entsteht, wenn man ein Bernoulli-Experiment mehrere Male wiederholt, und an der gesamten Anzahl der Erfolge interessiert ist.

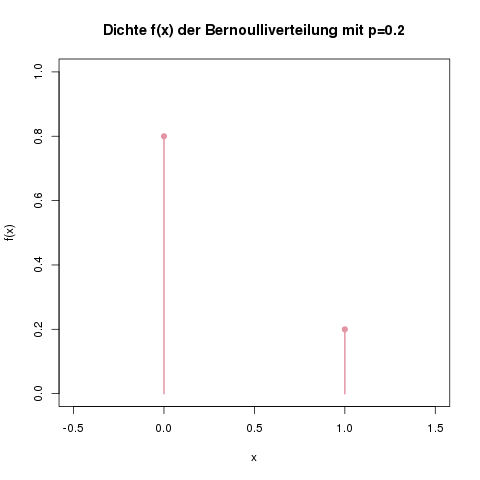
Im vorherigen Artikel zur Bernoulliverteilung haben wir ein Beispiel betrachtet, in dem wir auf einem Schießstand am Jahrmarkt einen einmaligen Schuß mit einer Trefferwahrscheinlichkeit von \(p=0.2\) abgeben. Wenn wir nun sechs Schüsse kaufen, folgt die Gesamtzahl der Treffer einer Binomialverteilung mit \(n=6\) und \(p=0.2\), oder:
\[ X \sim B(6, 0.2) \]

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Träger

Bei sechs Schüssen auf dem Schießstand können wir zwischen 0 und 6 jede Trefferzahl haben. Man darf hier die Null nicht vergessen, das kann leicht vorkommen. Es ist nämlich durchaus möglich, gar keine Treffer zu landen. Der Träger im allgemeinen Fall sind alle Ganzzahlen von \(0\) bis \(n\), also
\[ \mathcal{T} = \{0, 1, \ldots, n\} \]

Dichte

Die Dichte der Binomialverteilung mit den Parametern \(n\) und \(p\) lautet
\[ f(x) = {n \choose x} p^x (1-p)^{n-x} \]

Erinnert euch, dass für diskrete Zufallsvariablen die Bezeichnungen \(f(x)\) und \(\mathbb{P}(X=x)\) dasselbe bedeuten. Die Wahrscheinlichkeit für drei Treffer ist also \(\mathbb{P}(X=3)\), oder kurz \(f(3)\).

Der Wert \({n \choose k}\) ist dabei der Binomialkoeffizient, der im Artikel Mathematische Symbole erklärt wird, und auch in der Kombinatorik angewendet wird.

Wenn man versteht, wie diese Formel zustandekommt, kann man sie sich sogar selbst herleiten, und muss nicht in einer Formelsammlung nachsehen (wenn nicht, ist das aber auch nicht so schlimm).

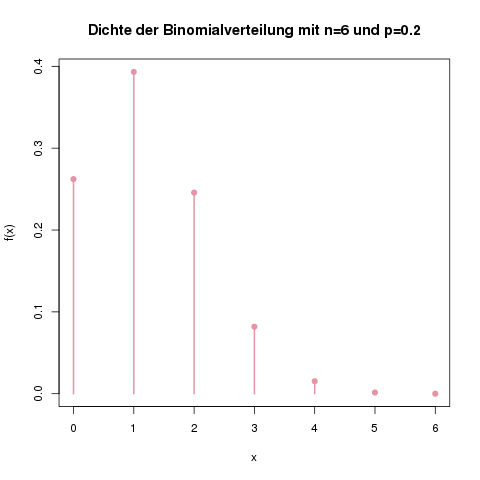
Die Dichte der Binomialverteilung mit n=6 und p=0.2. Man sieht, dass man mit hoher Wahrscheinlichkeit zwischen 0 und 3 Treffer erhalten wird. 5 oder 6 Treffer zu bekommen, ist sehr unwahrscheinlich.

Am Beispiel des Schießstandes: Die Wahrscheinlichkeit, dass wir zwei Treffer erhalten werden, ist laut Formel \(f(2) = {6 \choose 2} (0.2)^2 (0.8)^4\). Interpretiert wird das so:

Die Wahrscheinlichkeit für einen Treffer (kurz: „T“) ist 0.2, die für eine Niete (kurz: „N“) ist 0.8. Wenn wir nun die Wahrscheinlichkeit für die Ergebnisfolge „TTNNNN“ ausrechnen, multiplizieren wir die Wahrscheinlichkeiten, und landen bei \(0.2^2 \cdot 0.8^4\). Dies ist aber nur eine von vielen Möglichkeiten, zwei Treffer zu erhalten. Zum Beispiel liefern die Schussfolgen „TNNNNT“, oder „TNTNNN“ dasselbe Ergebnis, und haben alle dieselbe Wahrscheinlichkeit: \(0.2^2 \cdot 0.8^4\).

Wieviele solcher Folgen mit zwei Treffern aus sechs Schüssen gibt es nun? Es sind genau \({6 \choose 2} = 15\), wie im Artikel Kombinationen erklärt wird.

So erklärt man sich also nacheinander die drei Faktoren der Formel, zuerst \(p^x\) (die Wahrscheinlichkeit für einen Treffer, potenziert mit der Anzahl an Treffern), dann \((1-p)^{n-x}\) (die Wahrscheinlichkeit für eine Niete, potenziert mit der Anzahl an Nieten), und dann \(n \choose k\)

Zwischenaufgabe

Berechne für das Beispiel Schießstand die Wahrscheinlichkeit, gar keinen Treffer zu erhalten, und überprüfe anhand der Abbildung oben, ob das Ergebnis plausibel ist.

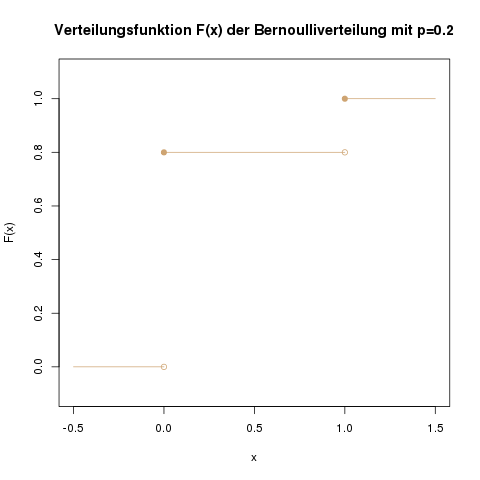
Verteilungsfunktion

Für die Verteilungsfunktion gibt es hier keine einfache Formel. In manchen Büchern (oder Klausuren) gibt es eine Verteilungstabelle zum einfachen Ablesen. In allen anderen Fällen muss man die einzelnen Wahrscheinlichkeiten also von Hand summieren. Das heisst, wenn man die Wahrscheinlichkeit für höchstens zwei Treffer berechnen möchte, also \(\mathbb{P}(X \leq 2)\), rechnet man sich die Wahrscheinlichkeit für null Treffer, einen Treffer, und zwei Treffer aus, und summiert sie:

\[ \begin{align*} \mathbb{P}(X \leq 2) &= \sum_{x=0}^2 \mathbb{P}(X = x) \\ &= \mathbb{P}(X = 0) + \mathbb{P}(X = 1) + \mathbb{P}(X = 2) \end{align*} \]

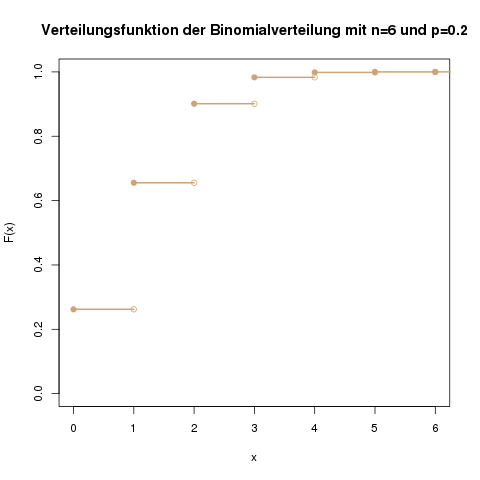
Anhand der Verteilungsfunktion kann man auch ablesen, dass die Wahrscheinlichkeit, höchstens 4 Treffer zu erhalten, schon nahezu 1 ist.

Zwischenaufgabe

Berechne die Wahrscheinlichkeit für höchstens fünf Treffer, d.h. \(\mathbb{P}(X \leq 5)\).

Das war ziemlich aufwändig, oder? Bei der Binomialverteilung gibt es einen Trick, der die Berechnung der Verteilungsfunktion oft schneller machen kann. Solche Aufgaben kommen oft in Klausuren vor, so dass man diesen Trick am besten verinnerlicht:

Statt alle Wahrscheinlichkeiten von \(x=0\) bis \(x=5\) aufzusummieren, kann man äquivalent die Wahrscheinlichkeiten aller „Gegenereignisse“, also in diesem Fall \(f(6)\), von 1 abziehen, und man erhält dieselbe Zahl. Denn wenn die Wahrscheinlichkeit für höchstens fünf Treffer 0.9999 ist, dann ist die Wahrscheinlichkeit für mehr als fünf (also 6) Treffer genau die Gegenwahrscheinlichkeit, d.h. 1-0.9999 = 0.0001.

Ein weiteres Beispiel (und wer das nachvollziehen kann, hat die Idee vollständig kapiert):

Uns interessiert nun die Wahrscheinlichkeit, zwischen einem und fünf Treffern (inklusive der eins und der fünf) zu erhalten. Die folgenden drei Formulierungen entsprechen den jeweiligen Formeln, und alle drei Formeln drücken genau dasselbe aus:

\(\mathbb{P}(1 \leq X \leq 5)\)

Die Wahrscheinlichkeit, eine Trefferzahl zwischen (inklusive) 1 und 5 zu erhalten

\(\mathbb{P}(X=1) + \mathbb{P}(X=2) + \mathbb{P}(X=3) + \mathbb{P}(X=4) + \mathbb{P}(X=5)\)

Die Wahrscheinlichkeit für einen, zwei, drei, vier, oder fünf Treffer

\(1 – \mathbb{P}(X=0) – \mathbb{P}(X=6)\)

Die Wahrscheinlichkeit, alles außer 0 und 6 Treffer zu erhalten

Ausrechnen kann man diesen Wert nun über die zweite oder dritte Formel dieser Liste. Es kommt natürlich dieselbe Zahl raus, wobei der letztere Weg der schnellere ist. Wichtig ist hier aber, dass man die Wahrscheinlichkeit für null Treffer, also \(f(0)\), nicht vergisst. Das passiert im Eifer des Gefechts nämlich gerne.

Erwartungswert

Der Erwartungswert der Binomialverteilung ist einfach:
\[ \mathbb{E}(X) = n \cdot p \]

Da der Erwartungswert für ein einzelnes Experiment \(p\) ist (siehe Bernoulliverteilung), erwartet man bei \(n\) Wiederholungen genau die \(n\)-fache Anzahl, also \(n\cdot p\) Treffer.

Varianz

Die Varianz der Binomialverteilung ist
\[ \mathbb{V}(X) = n \cdot p \cdot (1-p). \] Die Herleitung ist etwas aufwändiger, weshalb wir sie uns hier ersparen.

Mit der Bernoulliverteilung kann man Experimente modellieren, die wie folgt aufgebaut sind: Es handelt sich um ein einziges Experiment mit nur zwei möglichen Resultaten, die wir als 0 (für „Mißerfolg“) und 1 (für „Erfolg“) kodieren. Ein schönes Beispiel hierfür ist der Schießstand auf einem Jahrmarkt, bei dem man auf weiße Plastiksterne schießt und nur mit einer bestimmten Wahrscheinlichkeit (sagen wir 20%) trifft.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Die Wahrscheinlichkeit, mit der bei einem Experiment der Erfolg eintritt, wird mit dem Parameter \(p\) bezeichnet. Die mathematische Schreibweise für eine bernoulliverteilte Zufallsvariable \(X\) lautet

\[ X \sim \text{Be}(p) \]

Weitere Beispiele für bernoulliverteilte Zufallsvariablen sind die Roulettewette auf die Zahl 0 – hier wäre \(X \sim \text{Be}(\frac{1}{37})\) – oder der erste Spielzug im „Mensch ärgere dich nicht“, in dem man eine 6 würfeln muss, um eine Figur ins Spiel bringen zu dürfen; hier ist \(X \sim \text{Be}(\frac{1}{6})\).

Träger

Da es bei diesem Experiment nur zwei Ausgänge, nämlich „Erfolg“ (kodiert durch eine 1) und „Mißerfolg“ (kodiert durch eine 0) gibt, ist der Träger \(\mathcal{T}\) der Bernoulliverteilung die Menge \(\mathcal{T} = \{0,1\}\).

Dichte

Die Dichte besteht aus drei Teilen: Der Wahrscheinlichkeit für einen Erfolg, also \(\mathbb{P}(X=1)\) (das ist \(p\)), der Wahrscheinlichkeit für einen Mißerfolg, also \(\mathbb{P}(X=0)\) (das ist die Gegenwahrscheinlichkeit \(1-p\)), und einer 0 für alle anderen Werte von \(X\), d.h. überall anders:

\[ f(x) = \begin{cases} p, & x = 1 \\ 1-p, & x=0 \\ 0, &\text{sonst} \end{cases} \]

Die Dichte für unser Beispiel auf dem Jahrmarktschießstand. Die Wahrscheinlichkeit für eine Niete (also \(X=0\)) ist hier 80%, und die Wahrscheinlichkeit für einen Treffer, \(X=1\), ist 20%. Alle anderen Werte haben den Wert 0. Die Wahrscheinlichkeit, mit einem Schuss zum Beispiel 0.5 oder 3 Treffer zu erhalten, ist natürlich 0.

Verteilungsfunktion

Die Verteilungsfunktion ist \(F(x) = \mathbb{P}(X \leq x)\). In Worten heißt das: Die Wahrscheinlichkeit, dass das Ergebnis des Experiments kleiner oder gleich dem Wert \(x\) ist. Sie ist definiert in drei Abschnitten:

\[ F(x) = \begin{cases} 0, & x < 0 \\ 1-p, & x>=0 \, \text{und} \, x<1 \\ 1, & x \geq 1 \end{cases} \]

Der oberste Abschnitt beschreibt die erste Stufe: Unsere Variable \(X\) kann ja nur die Werte 0 oder 1 annehmen. Die Wahrscheinlichkeit, dass also eine Zahl kleiner als 0 herauskommt, ist natürlich 0. (Ebenso ist die Wahrscheinlichkeit, dass eine Zahl kleiner als z.B. -0.5 rauskommt, also \(F(-0.5)\), auch 0.

Die zweite Stufe ist der Bereich zwischen 0 und 1. Dort ist die Wahrscheinlichkeit, dass \(X \leq x\) ist, genau \(1-p\), und zwar aus dem Grund, dass nur die 0 (also ein Mißerfolg, oder auf unserem Schießstand „kein Treffer“) als mögliches Ergebnis kleiner oder gleich diesen Werten vorkommt – und der Mißerfolg hat die Wahrscheinlichkeit \(1-p\).

Die dritte Stufe ist alles über \(x=1\). Da nur die Ergebnisse 0 oder 1 rauskommen können, ist z.B. die Wahrscheinlichkeit dass \(X \leq 5\) ist, gleich 1. Die Funktion \(F(x)\) geht also ins Unendliche konstant mit dem Wert 1 weiter.

Die Verteilungsfunktion für das Beispiel des Jahrmarktschießstands ist eine Treppenfunktion. Hier liest man z.B. ab, dass \(\mathbb{P}(X \leq 0) = 0.8\) ist, und ebenso, dass \(\mathbb{P}(X \leq 0.5) = 0.8\) ist.

Erwartungswert

Der Erwartungswert der Bernoulliverteilung ist einfach: \(\mathbb{E}(X) = p\).

Das kann man sich über die Formel, die den Erwartungswert definiert, sofort herleiten:

\[ \mathbb{E}(X) = \sum_{i=1}^n x_i f(x_i) = 0 \cdot (1-p) + 1 \cdot p = p \]

Hier verwenden wir die beiden möglichen Ausprägungen \(x_1=0\) und \(x_2 = 1\), sowie deren Wahrscheinlichkeiten \(f(x_1) = 1-p\) (für Mißerfolg) und \(f(x_2) = p\) (für Erfolg).

Varianz

Die Varianz bei der Bernoulliverteilung ist \(\mathbb{V}(X) = p(1-p)\). Sie ist mit Hilfe ihrer Definition etwas aufwändiger zu bestimmen, aber auch noch machbar:

\[ \begin{align*} \mathbb{V}(X) &= \sum_{i=1}^n (x_i – \mu)^2 f(x_i) \\&=(x_1-p)^2 \cdot (1-p) + (x_2 – p)^2 \cdot p\\&=p^2 (1-p) + (1-p)^2 p \\&=(p^2 – p^3) + (1^2-2p+p^2)\cdot p \\&=p^2 – p^3 + p – 2p^2 + p^3 \\&=p – p^2 \\&=p(1-p) \end{align*} \]

Der Wert \(\mu\) ist hierbei, wie in der Definition beschrieben, eine Kurzschreibweise für den Erwartungswert \(\mathbb{E}(X) = p\).

Die diskrete Gleichverteilung liegt vor, wenn eine Zufallsvariable

• diskret ist, also das Experiment nur eine endliche Zahl an möglichen Ergebnissen hat, und
• jedes mögliche Ergebnis mit derselben Wahrscheinlichkeit auftritt.

Zwei schöne Beispiele hierfür sind der Münzwurf mit \(n=2\) möglichen Ergebnissen, Kopf oder Zahl, wo jedes mit der gleichen Wahrscheinlichkeit, \(\frac{1}{2}\), auftritt, und das Rouletterad mit \(n=37\) möglichen Ergebnissen (der Null und die Zahlen 1 bis 36), wo jede Zahl mit der Wahrscheinlichkeit \(\frac{1}{37}\) auftritt.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Parameter

Die möglichen Ergebnisse werden bezeichnet mit den Variablen \(x_1, x_2, \ldots, x_n\). Für das Beispiel des Münzwurfs können wir also „Kopf“ mit 1 kodieren, und „Zahl“ mit 2, und erhalten die möglichen Ergebnisse \(x_1=1, x_2=2\) (wir müssen diese Ereignisse in Zahlen umwandeln, der Grund ist im Artikel Was sind Zufallsvariablen? ganz oben erklärt.). Für das Roulette-Beispiel erhalten wir \(x_1=0, x_2=1, x_3=2, \ldots, x_{37}=36\).

Wir beschränken uns hier aber auf einen Spezialfall, nämlich Zufallsexperimente, deren Ergebnis jede Ganzzahl zwischen \(a\) und \(b\) sein kann. Beim Münzwurf haben wir also eine Gleichverteilung mit den zwei Parametern \(a=1\) und \(b=2\), und beim Roulettespiel eine Gleichverteilung mit \(a=0\) und \(b=36\). Mit dieser Art der Modellierung können wir die allermeisten Situationen modellieren, bis auf manche Sonderfälle, zum Beispiel das Punkteergebnis eines Fußballspiels, in dem ein Verein entweder 0, 1, oder 3 Punkte bekommt.

Träger

Der Träger \(\mathcal{T}\) der diskreten Gleichverteilung sind die einzelnen Ausprägungen \({x_1, x_2, \ldots, x_n}\), also alle ganzen Zahlen zwischen \(a\) und \(b\). Beim Roulettespiel sind das z.B. die Zahlen \({0, 1, 2, \ldots, 36}\). Andere Ergebnisse sind in diesem Beispiel nicht möglich: Das Rouletterad kann zum Beispiel keine 52, oder keine 3,5 zeigen.

Dichte

Die Dichtefunktion muss in zwei Teile aufgeteilt werden. Beim Roulettespiel ist z.B. die Wahrscheinlichkeit, dass die 17 erscheint, \(\mathbb{P}(X=17) = \frac{1}{37}\), aber die Wahrscheinlichkeit, dass das Ergebnis 1500 ist, \(\mathbb{P}(X=1500) = 0\). Die Dichte für das Roulettespiel ist also

\[ f(x) = \begin{cases} \frac{1}{37}, & x \in \{0, 1, \ldots , 36\} \\ 0, & \text{sonst} \end{cases} \]

Im Allgemeinen haben wir \(n\) verschiedene Ergebnisse für eine Zufallsvariable, die wir mit \(x_1, x_2, \ldots, x_n\) bezeichnen (also wieder alle Zahlen von \(a\) bis \(b\), den Träger). Hier ist die Dichte dann

\[ f(x) = \begin{cases} \frac{1}{n}, & x \in \{ a, a+1, \ldots , b \} \\ 0, & \text{sonst} \end{cases} \]

Verteilungsfunktion

Die Verteilungsfunktion der diskreten Gleichverteilung lautet wie folgt:

\[ F(x) = \begin{cases} 0, & x < a \\ \frac{\lfloor x \rfloor – a + 1}{b-a+1}, & x \in [a,b]\\ 1, & x > b \end{cases}\]

„Links“ von \(a\) ist die Verteilungsfunktion also immer 0, und „rechts“ von \(b\) ist sie immer 1. Mit \(\lfloor x \rfloor\) ist hier die Abrundung von \(x\) gemeint, also ist z.B. \(\lfloor 3.4 \rfloor = 3\) und \(\lfloor 5 \rfloor = 5\).

Möchten wir für das Roulettespiel z.B. bestimmen, mit welcher Wahrscheinlichkeit eine Zahl kleiner oder gleich 3.5 kommt, bestimmen wir:

\[ F(3.5) = \frac{\lfloor 3.5 \rfloor – 0 + 1}{36 – 0 + 1} = \frac{4}{37} \]

Versuche, mit dieser Definition für das Beispiel Würfelwurf zu bestimmen:

• \(F(4)\), also die Wahrscheinlichkeit, mit der wir eine Augenzahl würfeln, die kleiner oder gleich 4 ist.
• \(F(4.8)\)
• \(F(0)\)
• \(F(1500)\)

Erwartungswert

Der Erwartungswert ist bei der diskreten Gleichverteilung einfach der Mittelwert von \(a\) und \(b\):

\[ \mathbb{E}(X) = \frac{a+b}{2} \]

Varianz

Die Varianz dieser Verteilung lautet:

\[ \mathbb{V}(X) = \frac{(b-a+1)^2 – 1}{12} \]

Beispielaufgabe

Schauen wir uns die Zufallsvariable „\(X\) = ein Würfelwurf“ an, und bestimmen für sie

• Träger
• Dichte
• Verteilungsfunktion
• Erwartungswert
• Varianz

Träger

Die Zufallsvariable \(X\) kann nur die Werte 1, 2, 3, 4, 5, oder 6 annehmen. Also ist der Träger \(\{ 1, 2, 3, 4, 5, 6 \}\).

Dichte

Die Dichte ist, wenn wir die obige Definition anwenden, einfach bestimmt:

\[ f(x) = \begin{cases} \frac{1}{6}, & x \in \{ 1, 2, 3, 4, 5, 6 \} \\ 0, & \text{sonst} \end{cases} \]

Dichte der diskreten Gleichverteilung beim Experiment „Werfen eines Würfels“. Jedes Ereignis von 1 bis 6 tritt mit der gleichen Wahrscheinlichkeit \(\mathbb{P}(X=i) = \frac{1}{6}\) auf.

Verteilungsfunktion

Die Verteilungsfunktion ist einfach notierbar als:

\[ F(x) =\begin{cases}0, & x < 1\\ \frac{\lfloor x \rfloor}{6},& 1 \leq x <6\\ 1, & x \geq 6 \end{cases}\]

Erwartungswert

Der Erwartungswert eines Würfelwurfs ist

\[ \mathbb{E}(X) = \frac{1}{2} (6 + 1) = 3.5 \]

Varianz

Auch hier sind wir schnell am Ziel. Die Formel angewendet lautet

\[ \mathbb{V}(X) = \frac{(6-1+1)^2 – 1}{12} = 2.917 \]