Bisher haben wir uns mit der deskriptiven (oder beschreibenden) Statistik, sowie mit der Wahrscheinlichkeitsrechnung beschäftigt:
- In der deskriptiven Statistik haben wir eine Stichprobe, und beschreiben ihre Eigenschaften (z.B. Mittelwerte, Varianzen, oder Quantile in einem Boxplot). Wichtig hier: Wir beschreiben nur die Stichprobe. Es werden keine Aussagen über die Grundgesamtheit, aus der die Stichprobe kommt, getroffen.
- In der Wahrscheinlichkeitsrechnung haben wir eine gegebene Verteilung inklusive aller ihrer Parameter, und möchten die Wahrscheinlichkeit bestimmen, mit der zukünftige Daten bestimmte Werte annehmen.
In der Inferenzstatistik (oft auch induktive oder schließende Statistik genannt) gehen wir nun genau andersrum wie in der Wahrscheinlichkeitsrechnung vor: Wir haben eine Stichprobe gegeben, und möchten mit ihrer Hilfe auf die Parameter der darunterliegenden Verteilung in der Grundgesamtheit schließen.
Die Inferenzstatistik verbindet also die vorhergehenden beiden Teile. Wir berechnen Kennzahlen der Stichprobe (deskriptiv), und schließen dann mit Hilfe der Wahrscheinlichkeitsrechnung auf Eigenschaften in der Grundgesamtheit.
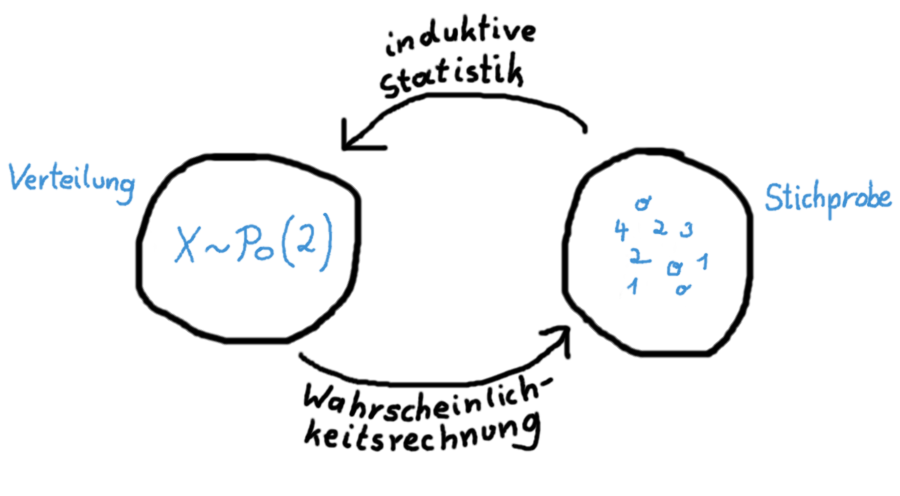
In der Wahrscheinlichkeitsrechnung haben wir eine Verteilung gegeben und wollen die Wahrscheinlichkeit für gewisse Daten ausrechnen. In der Inferenzstatistik haben wir Daten gegeben und wollen deren Verteilung (hier: Eine Poissonverteilung mit Parameter \(\lambda=2\)) bestimmen.
Sowohl Hypothesentests als auch Regressionsmodelle kommen aus der Inferenzstatistik. Um in diesem Rahmen Inferenz zu betreiben, muss man zuerst eine den Daten unterliegende Verteilung annehmen. Dazu bedienen sich beide Verfahren statistischer Modelle.
Ein statistisches Modell ist eine (idealisierte) Annahme über das System (meistens: eine bestmmte Verteilung), das einen bestimmten Datensatz generiert hat. Unter der Annahme, dass die Stichprobe zufällig aus der Grundgesamtheit entnommen wurde, gilt dasselbe Modell dann für Stichprobe sowie Grundgesamtheit. Dadurch lässt sich Inferenzstatistik betreiben, und es lassen sich aus der Stichprobe Schlussfolgerungen über die Grundgesamtheit ziehen.
Wie gesagt: zwei große Teilgebiete der Inferenzstatistik sind in den einführenden Statistikveranstaltungen besonders wichtig:
- Zum einen das Schätzen der genauen Parameter (wie z.B. den Wert \(\lambda=2\) in der oberen Grafik) bzw. Bereiche, in denen der Parameter höchstwahrscheinlich liegt (sogenannter Konfidenzintervalle)
- Zum anderen das Testen, ob gewisse Parameter einen bestimmten, hypothetischen Wert annehmen.
Beim Schätzen haben wir also keine vorherige Meinung, was der Parameter sein könnte, und berechnen einfach einen höchstwahrscheinlichen Wert aus den Daten, und beim Testen haben wir vorher eine Idee über den Parameter (z.B. behaupten wir, dass \(\lambda=3\) ist), und überprüfen die Plausibilität dieser Behauptung (oder Hypothese) in einem Test.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hey Alex, wenn du mal wieder Zeit findest wäre es super wenn du die induktive Statistik ausbauen könntest, dazu gibt es einfach nichts verständliches. Ich hatte mich schon gefreut auf deine Inhaltsübersicht, ehe ich feststellen musste, dass die für mich interessanten Unterpunkte nicht klickbar sind :/
Super geniale Seite, ist ne tolle Ergänzung zu den Vorlesungsunterlagen und leicht verständlich. Danke für die Mühe 🙂
Was für eine geniale Seite! Ich dachte, ich hätte mit Bestehen der Statistikklausur damals dieses Kapitel für immer schließen können, doch jetzt kam die Masterarbeit -.- Dann warte ich mal auf die Inhalte der Inferenzstatistik. Tausenddank!!
Hallo Alex,
danke auch von mir für deine Website!
Eine Frage: Die Inhalte zur Inferenzstatisik (z. B. Parameterschätzung und KIs) sind wohl noch nicht fertig oder finde ich es nur nicht?
Liebe Grüße,
Anne
Die sind noch in Arbeit, richtig 🙂
Hi Alex!
Erstmal möchte ich sagen, dass deine Erklärungen wirklich die besten sind die ich finden konnte. Vielen Dank dafür!
Wann in etwa wirst du den inferenzstatistischen Teil veröffentlichen?
LG Konstantin
Das könnte noch ein bisschen dauern, sorry :/ Momentan habe ich recht wenig Zeit für dieses Hobby…
Oh mann, du bist einfach geil ! Dank dir bin ich bereit für die Statistik-Klausur… jetzt fehlt mir nur noch ‚Induktive Statistik‘ 😀
Einfach nur wunderbar!!! Ich studiere BWL im fünften Semester und bin bisher schon zwei mal an Statistik gescheitert und war gerade zu am verzweifeln, denn wie du schön schreibst „Mathematiker verstehen ihre Materie oft anders als Nicht-Mathematiker“ und in meinem Fall bin ich wirklich eher der Wirtschaftswissenschaftler… Aber das Modul gehört leider dazu, was schon einigen von uns zum Verhängnis wurde.
Vielen Dank auch im Namen meiner Kommilitonen, denen ich dich gleich empfohlen habe und ich hoffe, dass es dieses Mal was wird mit bestehen 🙂
Bitte mach weiter so!!!
Aww. 😀