In diesem Artikel schauen wir uns stetige Zufallsvariablen im Allgemeinen an. Spezielle Verteilungen wie die Exponentialverteilung oder Normalverteilung findet man im Abschnitt „Verteilungen“ im Inhaltsverzeichnis.
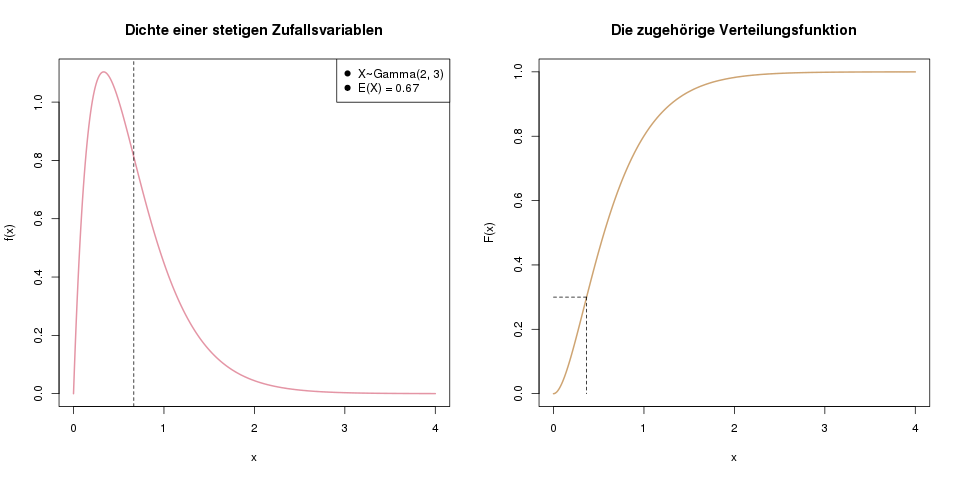
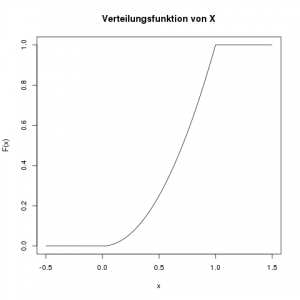
Im linken Bild sieht man ein Beispiel einer Dichte für eine stetige Zufallsvariable. Die gestrichelte Linie markiert den Erwartungswert von X. Rechts ist die Verteilungsfunktion derselben Zufallsvariablen abgebildet. Die gestrichelte Linie hier markiert das 30%-Quantil, das wir genau wie bei diskreten Zufallsvariablen bestimmen.
Dichte
Jede Dichtefunktion einer stetigen Zufallsvariablen hat zwei Eigenschaften:
- Die Funktion hat nirgends einen negativen Wert, ist also auf den gesamten reellen Zahlen entweder 0 oder größer als 0. Mathematisch ausgedrückt: \(f(x) \geq 0\) für alle \(x \in \mathbb{R}\).
- Die Fläche unter der gesamten Dichtefunktion (ihr Integral) ergibt 1. Das ist analog zur Dichte bei diskreten Zufallsvariablen, wo die Summe aller ihrer einzelnen Wahrscheinlichkeiten 1 ergibt.
Der große Unterschied zwischen diskreten und stetigen Zufallsvariablen ist, dass die Dichte hier, bei stetigen Zufallsvariablen, nicht die Wahrscheinlichkeit für einen beliebigen Punkt repräsentiert. Im stetigen Fall ist es nun so, dass die Wahrscheinlichkeit für ein bestimmtes, festes Ergebnis immer Null ist. Im Beispielbild oben ist etwa \(\mathbb{P}(X=0.237) = 0\).
Im stetigen Fall kann man Wahrscheinlichkeiten nur für Intervalle bestimmen. Man kann also z.B. sagen, dass \(X\) mit 18.2% einen Wert zwischen 1 und 2 annehmen wird: \(\mathbb{P}(X \in [1,2]) = 0.182\). Diese „Wahrscheinlichkeitsmasse“ von 0.182 ist die Fläche unter der Dichte, von 1 bis 2.
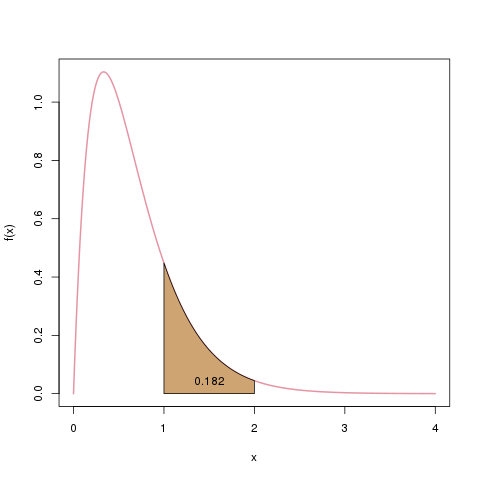
Die Wahrscheinlichkeit, dass das Ergebnis unserer Zufallsvariablen zwischen 1 und 2 liegt, notieren wir mit \(\mathbb{P}(X \in [1,2])\). Wir bestimmen es als die Fläche unter der Dichte, beschränkt auf den Bereich \([1,2]\), hier als braune Fläche dargestellt.
Verteilungsfunktion
Die Verteilungsfunktion \(F(x)\) ist im stetigen Fall genauso definiert wie im diskreten Fall:
\[ F(x) = \mathbb{P}(X \leq x) \]
Sie wird jetzt nicht über die Summe der Dichte berechnet, sondern weil wir ja unendlich mögliche Werte für \(x\) haben, über das Integral der Dichte berechnet.
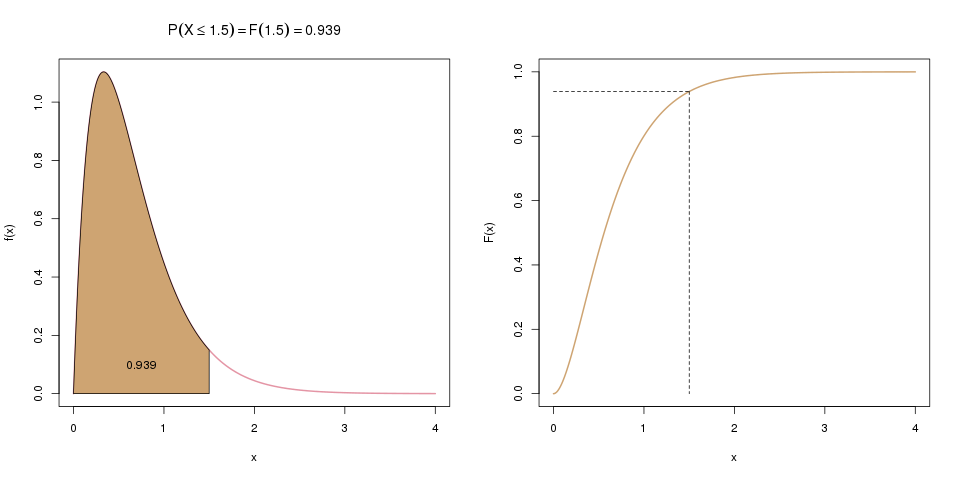
Links sieht man die Dichtefunktion. Die Wahrscheinlichkeit, dass \(X\) kleiner oder gleich 1.5 ist, entspricht der Fläche unter der Dichte bis zum Wert 1.5 auf der x-Achse. Rechts ist die Verteilungsfunktion \(F(x)\) abgebildet, die genau diese Fläche darstellt.
Es gilt also:
\[ F(x) = \int_{-\infty}^x f(t) dt \]
Wer sich nun wundert, warum wir auf einmal \(f(t)\) statt \(f(x)\) schreiben: Weil wir das \(x\) schon für die Verteilungsfunktion \(F\) verwenden, müssen wir uns bei der Dichte kurzfristig einen neuen Buchstaben überlegen. Ähnlich wie beim Summenzeichen \(\sum\), bei der man meistens die Indexvariable \(i\) einführt, wird hier temporär das Argument \(t\) statt \(x\) verwendet. Der Funktion \(f\) ist es ja egal, wie ihr Argument heißt, sie verarbeitet es einfach und spuckt ihr Ergebnis aus, nämlich die Dichte an dieser Stelle, sei es nun beispielhaft \(x=2.5\) oder \(t=2.5\).
Möchten wir also die Wahrscheinlichkeit wissen, dass \(x\) kleiner oder gleich 1.5 ist, berechnen wir \(\int_{-\infty}^{1.5} f(t) dt\). Das Integral startet immer bei \(-\infty\), egal wo die Dichte tatsächlich beginnt. Die Schreibweise ist einfach allgemeingültiger, für alle möglichen Dichten. Das macht in unserem Fall auch nichts aus, weil \(f(t)\) hier im negativen Bereich 0 ist, also keine Fläche hat.
Oft interessiert uns aber auch die Wahrscheinlichkeit, dass \(X\) zwischen zwei Werten, z.B. zwischen 0.5 und 1.5 liegt. Die Verteilungsfunktion liefert uns aber nur die Wahrscheinlichkeit, dass \(X\) kleiner/gleich einem Wert ist. Hier können wir aber einen Trick anwenden: Wenn wir zuerst \(F(1.5)\) berechnen, und davon dann \(F(0.5)\) abziehen, haben wir genau die gesuchte Wahrscheinlichkeit, \(\mathbb{P}(0.5 \leq X \leq 1.5)\). Die folgenden zwei Bilder ergänzen das erste Bild von oben und visualisieren diese Idee:
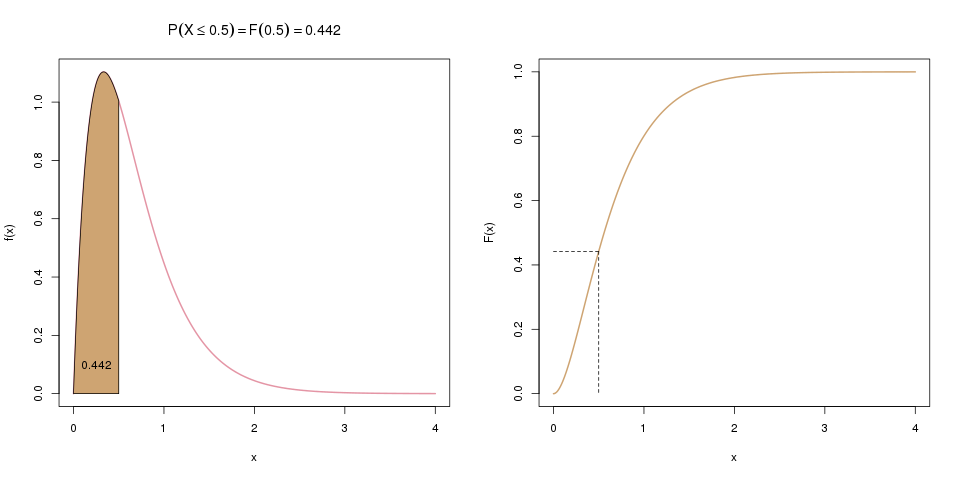
Im ersten Schritt (weiter oben) berechneten wir \(\mathbb{P}(X \leq 1.5)\). Hier, im zweiten Schritt, berechnen wir nun \(\mathbb{P}(X \leq 0.5)\), was hier links als braune Fläche dargestellt wird, und rechts als entsprechender Wert der Verteilungsfunktion.
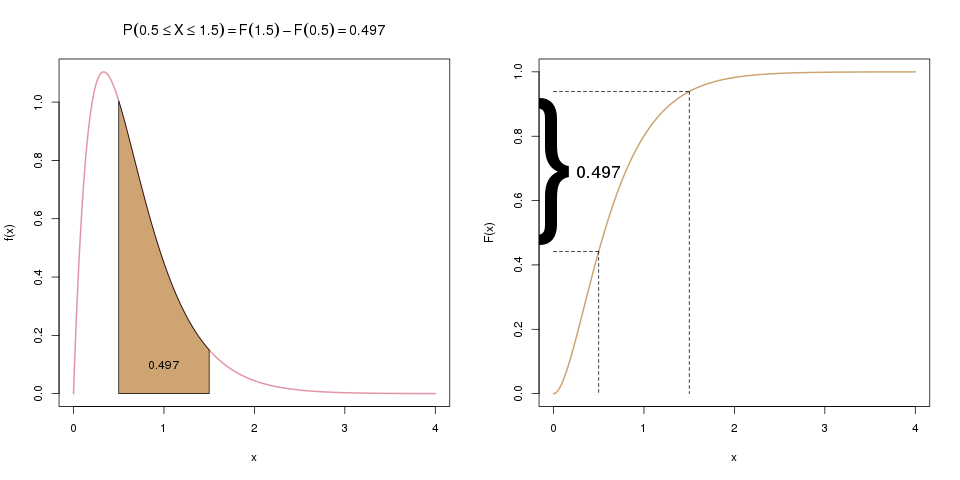
Im letzten Schritt ziehen wir \(F(0.5)\) von \(F(1.5)\) ab. Übrig bleibt die gesuchte Wahrscheinlichkeit \(\mathbb{P}(0.5 \leq X \leq 1.5)\), die im linken Bild als Fläche dargestellt ist, und im rechten als Differenz der beiden Werte auf der y-Achse.
Formel oder Verteilungstabelle?
Die Dichte von allen relevanten Zufallsvariablen ist immer als Formel darstellbar. Es ist zum Beispiel für eine normalverteilte Variable \(X\) die Dichte \(f(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp(-\frac{(x-\mu)^2}{2\sigma^2})\). Bei der Verteilungsfunktion ist das allerdings nicht immer der Fall. Für die Exponentialverteilung existiert eine Formel für die Verteilungsfunktion, da es ein einfach zu berechnendes Integral ist. Für die Normalverteilung allerdings lässt sich die Verteilungsfunktion nicht einfach hinschreiben. In diesem Fall gibt es Verteilungstabellen, die z.B. in 0.01er-Schritten den Wert von \(F(x)\) tabelliert haben. Muss man also von Hand (und das passiert eigentlich nur noch in Klausuren) die Verteilungsfunktion einer Zufallsvariablen bestimmen, kommt es auf die Verteilung an, ob man eine Formel an einem bestimmten Wert \(x\) auswertet, oder in einer Verteilungstabelle für einen bestimmten Wert \(x\) nachsieht.
Quantilsfunktion
Die Quantilsfunktion \(Q(x)\) (manche nennen sie auch einfach nur \(F^{-1}(x)\)) bei stetigen Zufallsvariablen ist nichts anderes als die Umkehrfunktion der Verteilungsfunktion. Die Umkehrfunktion von einer beliebigen Funktion \(y=F(x)\) wird mit \(x=F^{-1}(y)\) bezeichnet. Das bedeutet aber nicht \(\frac{1}{F(x)}\), sondern dass sie von einem Funktionswert \(y\) zurück auf den ursprünglichen Wert \(x\) führt.
Die Umkehrfunktion von \(y=2x+3\) ist zum Beispiel \(x=\frac{1}{2}(y-3)\). Man bildet sie, indem man in der ursprünglichen Formel nach \(x\) auflöst:
\[ \begin{align*} y &= 2x+3\\ y-3 &= 2x \\ \frac{1}{2}(y-3) &= x \end{align*} \]
Genauso macht man das bei der Quantilsfunktion: Man löst die Formel der Verteilungsfunktion nach \(x\) auf. Voraussetzung dafür ist natürlich, dass die Verteilungsfunktion als Formel darstellbar ist. Wenn nicht, muss man (wie oben erklärt) wieder auf Tabellen zurückgreifen. Klassischer Fall dafür ist die Normalverteilung, deren Quantile beim Testen wichtig sind.
Umwandeln von der Dichte zur Verteilungsfunktion/Quantilsfunktion und wieder zurück
Eine Zufallsvariable ist schon eindeutig beschrieben, wenn man nur eine der drei Funktionen (Dichte, Verteilungsfunktion, oder Quantilsfunktion) hat. Man kann nämlich eindeutig zwischen den dreien hin- und herrechnen:
- Die Dichte ist die Ableitung der Verteilungsfunktion: \[ f(x) = \frac{d}{dx} F(x) \]
- Die Verteilungsfunktion ist die Fläche unter der Dichte, d.h. das Integral der Dichte: \[ F(x) = \int_{-\infty}^x f(t) dt \]
- Die Quantilsfunktion ist die Umkehrfunktion der Verteilungsfunktion: \[ Q(x) = F^{-1}(x) \]
- Die Verteilungsfunktion ist die Umkehrfunktion der Quantilsfunktion: \[ F(x) = Q^{-1}(x) \]
Erwartungswert
Hinter dem Erwartungswert einer stetigen Zufallsvariable steckt genau dieselbe Idee wie im diskreten Fall. Hier wird lediglich statt der Summe ein Integral verwendet. Im diskreten Fall haben wir über alle möglichen Ausprägungen \(x_i\) multipliziert mit der zugehörigen Dichte \(f(x_i)\) summiert, und hier werden wir stattdessen über alle Ausprägungen \(x\) multipliziert mit der Dichte \(f(x)\) integrieren:
\[ \mathbb{E}(X) = \int_{-\infty}^\infty x \cdot f(x) \; dx \]
Varianz und Standardabweichung
Auch die Varianz ist im stetigen Fall ähnlich aufgebaut wie bei diskreten Zufallsvariablen:
\[ \mathbb{V}(X) = \int_{-\infty}^\infty (x-\mu)^2 f(x) dx, \]
wobei \(\mu = \mathbb{E}(X) = \int_{-\infty}^\infty x f(x) dx\). Man muss zur Berechnung der Varianz also vorher den Erwartungswert bestimmt haben.
Meistens ist es einfacher, statt diesem komplizierten Integral den Verschiebungssatz anzuwenden. Die Varianz ist äquivalent bestimmbar als
\[ \mathbb{V}(X) = \mathbb{E}(X^2) – \mathbb{E}(X)^2. \]
Dabei ist der zweite Teil, \(\mathbb{E}(X)^2\), einfach das Quadrat des Erwartungswertes, aber der erste Teil, \(\mathbb{E}(X^2)\), etwas ganz anderes, nämlich der Erwartungswert von \(X^2\). Das ist eine Transformation der Zufallsvariablen \(X\), deren Erwartungswert wir mit der Transformationsregel bestimmen können:
\[ \mathbb{E}(X^2) = \int_{-\infty}^\infty x^2 f(x) \, dx \]
Dieses Integral ist leichter zu berechnen als das vorherige, und wenn man den Erwartungswert eh schon bestimmt hat, ist man mit dieser Methode meist schneller am Ziel. In der folgenden Beispielaufgabe bestimmen wir u.a. die Varianz, und verwenden beide Methoden, um den Unterschied zu sehen.
Beispielaufgabe
Als Beispiel schauen wir uns eine Zufallsvariable \(X\) und ihre Dichte \(f(x)\) an:
\[ f(x) = \begin{cases} 2x &\mbox{falls } 0 \leq x \leq 1 \\ 0 & \mbox{sonst} \end{cases} \]
Für diese Dichte werden wir nun
- die Funktion skizzieren
- nachweisen, dass es sich tatsächlich um eine Dichte handelt
- ihren Träger bestimmen
- den Erwartungswert berechnen
- die Varianz berechnen
- ihre Verteilungsfunktion bestimmen
- ihre Quantilsfunktion bestimmen
- die Wahrscheinlichkeit, dass \(X\) zwischen 0.5 und 0.6 liegt, bestimmen
Skizze der Funktion
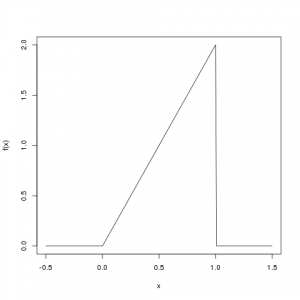
Die Dichte \(f(x)\) ist nur im Bereich von 0 bis 1 ungleich Null:
Ist es tatsächlich eine Dichte?
Um nachzuweisen dass eine Funktion \(f(x)\) eine „echte“ Dichte ist, müssen wir zwei Eigenschaften überprüfen:
- Die Funktion darf auf den kompletten reellen Zahlen nicht negativ sein: \(f(x) \geq 0\) für alle \(x \in \mathbb{R}\).
- Das Integral der Dichte, über die gesamten reellen Zahlen, muss 1 ergeben: \(\int_{-\infty}^\infty f(x) dx = 1\).
Die erste Eigenschaft ist schnell nachgewiesen: Im Bereich von 0 bis 1 ist \(2x > 0\), und im übrigen Bereich ist die Funktion 0, das ist also okay. Man sieht das auch auf der Skizze oben.
Um die zweite Eigenschaft nachzuweisen müssen wir also die Dichte integrieren. Zuerst teilen wir das Integral von \(-\infty\) bis \(\infty\) in drei Teile auf:
\[ \begin{align*} \int_{-\infty}^\infty f(x) dx &= \int_{-\infty}^0 0 \, dx \\ &+ \int_0^1 2x \, dx \\ &+ \int_1^\infty 0 \, dx \end{align*} \]
Der erste und dritte Teil fällt sofort weg: Die Fläche unter der Funktion, die konstant Null ist, ist natürlich auch Null. Wir integrieren also nur den Teil von 0 bis 1:
\[ \begin{align*} \int_{-\infty}^\infty f(x) dx &= \int_0^1 2x \, dx \\ &= \left[ 2 \cdot \frac{1}{2} x^2 \right]^1_0 \\ &= 2\cdot \frac{1}{2} \cdot 1^2 – 2 \cdot \frac{1}{2} 0^2 = 1-0 = 1 \end{align*} \]
Das Integral ist also insgesamt 1, und damit ist \(f(x)\) eine echte Dichte.
Was ist der Träger der Zufallsvariablen?
Der Träger einer Zufallsvariablen ist einfach die Menge aller möglichen Ergebnisse von \(X\). Übersetzt bedeutet das: Der Bereich, in dem der Funktionswert \(f(x)\) (also der Wert auf der \(y\)-Achse) größer als 0 ist. In unserem Fall also das Intervall von 0 bis 1 (strikt gesagt ohne der Null). Somit ist der Träger \(\mathcal{T} = (0,1]\).
Was ist ihr Erwartungswert \(\mathbb{E}(X)\)?
Für den Erwartungswert wenden wir die Formel von oben an. Wir teilen das Integral wieder in drei Teile auf, wobei die Teile von \(-\infty\) bis \(0\) sowie von \(1\) bis \(\infty\) wieder wegfallen (da die Dichte dort 0 ist, und somit das Integral 0 wird):
Vorsicht: Im Integral steht hier nicht nur \( f(x) \), sonst wäre die Lösung des Integrals ja 1, sondern \( x \cdot f(x) \).
\[ \begin{align*} \mathbb{E}(X) = \int_{-\infty}^\infty x f(x) \, dx &= \int_{-\infty}^0 x \cdot 0 \, dx + \int_0^1 x \cdot 2x \, dx + \int_1^\infty x \cdot 0 \, dx \\ &= \int_0^1 x \cdot 2x \, dx \\ &= \int_0^1 2x^2 \, dx \\ &= \left[ 2\cdot \frac{1}{3} x^3 \right]^1_0 \\ &= 2 \cdot \frac{1}{3} 1^3 – 2 \cdot \frac{1}{3} 0^3 \\ &= \frac{2}{3} \end{align*} \]
Somit ist \(\mathbb{E}(X) = \frac{2}{3}\).
Was ist ihre Varianz \(\mathbb{V}(X)\)?
Die Varianz können wir mit zwei Methoden bestimmen. Zuerst verwenden wir die Methode mit Verschiebungssatz:
\[ \mathbb{V}(X) = \mathbb{E}(X^2) – \mathbb{E}(X)^2 \]
Da \(\mathbb{E}(X)=\frac{2}{3}\), ist der zweite Term hier schon bekannt: \(\mathbb{E}(X)^2 = (\frac{2}{3})^2 = \frac{4}{9}\).
Für den ersten Teil wenden wir die Transformationsregel an. Das Integral ist wieder nur im Bereich von 0 bis 1 ungleich Null, also interessiert uns nur dieser Bereich. Es ist ein häufiger Fehler, die Grenzen des Integrals bei \(-\infty\) und \(\infty\) zu lassen, was die Lösung dann unmöglich macht, hier also aufpassen!
\[ \begin{align*} \mathbb{E}(X^2) &= \int_{-\infty}^\infty x^2 f(x) \, dx \\ &= \int_0^1 x^2 \cdot 2x \, dx \\ &= \int_0^1 2x^3 \, dx \\ &= \left[ 2 \frac{1}{4} x^4 \right]^1_0 = \frac{1}{2} \end{align*} \]
Und damit können wir die Varianz bestimmen:
\[ \mathbb{V}(X) = \mathbb{E}(X^2) – \mathbb{E}(X)^2 = \frac{1}{2} – \frac{4}{9} = \frac{9}{18} – \frac{8}{18} = \frac{1}{18} \]
Damit sind wir fertig: \(\mathbb{V}(X) = \frac{1}{18}\).
Nur um zu sehen, wie kompliziert es ohne dieser Regel ist, berechnen wir die Varianz hier nocheinmal mit der ursprünglichen Formel (ich ersetze hier \(\mathbb{E}(X)\) mit \(\mu\), damit die Notation übersichtlicher wird). Wer noch Schwierigkeiten beim Integrieren hat, kann natürlich auf dem Papier mitrechnen:
\[ \begin{align*} \mathbb{V}(X) = \int_{-\infty}^\infty (x-\mu)^2 f(x) \, dx &= \int_0^1 (x^2 – 2\mu x + \mu^2) \cdot 2x \, dx \\ &= \int_0^1 2x^3-4\mu x^2 + 2\mu^2 x \, dx \\ &= \left[ 2 \cdot \frac{1}{4} x^4 – 4 \mu \cdot \frac{1}{3} x^3 + 2\mu^2 \cdot \frac{1}{2} x^2 \right]_0^1 \\ &= (2 \cdot \frac{1}{4} 1^4 – 4\mu \cdot \frac{1}{3}1^3 + 2\mu^2 \cdot \frac{1}{2} 1^2) – (0-0+0) \\ &= \frac{2}{4} – \frac{4}{3}\mu + \frac{2}{2}\mu^2 \\ &= \frac{1}{2} – \frac{4}{3} \cdot \frac{2}{3} + \left( \frac{2}{3} \right)^2 \\ &= \frac{1}{2} – \frac{8}{9} + \frac{4}{9} \\ &= \frac{9}{18} – \frac{16}{18} + \frac{4}{9} \\ &= \frac{1}{18} \end{align*} \]
Was ist ihre Verteilungsfunktion \(F(x)\)?
Die Verteilungsfunktion an der Stelle \(x\) ist die Fläche der Dichte, links von der Stelle \(x\). Wir integrieren also die Dichte von \(-\infty\) bis \(x\). Da die Variable \(x\) hier die rechte Grenze der Fläche angibt, müssen wir in der Dichtefunktion einen anderen Variablennamen nehmen, wir verwenden einfach \(t\). Das ändert natürlich die Funktion nicht, denn ob da \(f(x)=2x\) oder \(f(A) = 2A\) steht, ist egal.
Da die Dichte stückweise definiert ist, d.h. einmal von \(-\infty\) bis \(0\), dann von \(0\) bis \(1\), und schließlich von \(1\) bis \(\infty\), müssen wir auch die Verteilungsfunktion getrennt in diesen Stücken definieren.
Die Fläche unter der Dichte von \(-\infty\) bis \(0\) ist Null: \(F(x) = 0 \; \text{falls} \; x \leq 0\).
Für den Bereich von 0 bis 1 müssen wir wieder ein Integral lösen:
\[ \begin{align*} F(x) &= \int_0^x f(t) \, dt \\ &= \int_0^x 2t \, dt \\ &= \left[ 2 \cdot \frac{1}{2} t^2 \right]_0^x \\ &= \frac{2}{2} x^2 – \frac{2}{2} 0^2 \\ &= x^2 \end{align*} \]
Und schließlich, im Bereich von \(1\) bis \(\infty\) ist \(F(x)\) konstant, weil die Dichte dort 0 ist. Der Wert von \(F(x)\) ist hier konstant 1, da z.B. \(\mathbb{P}(X \leq 123) = 1\).
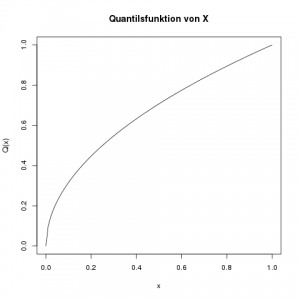
Was ist die Quantilsfunktion \(Q(x)\)?
Die Quantilsfunktion ist nur von 0 bis 1 definiert, und ist in diesem Bereich die Umkehrfunktion der Verteilungsfunktion \(F(x)\). Um die Umkehrfunktion zu berechnen, ersetzen wir in der Definition der Verteilunsfunktion \(F(x)\) durch \(x\), und \(x\) durch \(Q(x)\):
\[ \begin{align*} F(x) &= x^2 \\ x &= \left(Q(x)\right)^2 \end{align*}\]
Das lösen wir jetzt nach \(Q(x)\) auf:
\[ \sqrt{x} = Q(x)\]
Und das ist auch schon die Quantilsfunktion (nicht vergessen, nur im Bereich von 0 bis 1!)
Was ist die Wahrscheinlichkeit, dass \(X\) zwischen 0.5 und 0.6 liegt?
Wir möchten also \(\mathbb{P}(0.5 \leq X \leq 0.6)\) bestimmen. Hierfür gibt es wieder eine einfache, und eine aufwändige Methode. In der einfachen Methode arbeiten wir mit der Verteilungsfunktion:
\[ \begin{align*} \mathbb{P}(0.5 \leq X \leq 0.6) &= \mathbb{P}(X \leq 0.6) – \mathbb{P}(X \leq 0.5) \\ &= F(0.6)-F(0.5) \\ &= 0.6^2 – 0.5^2 \\ &= 0.36-0.25 \\ &= 0.11 \end{align*} \]
Die Wahrscheinlichkeit liegt also bei 0.11.
In der komplizierteren Variante würden wir die Fläche unter der Dichte im Bereich von 0.5 bis 0.6 bestimmen, wir würden also das folgende Integral lösen:
\[ \int_{0.5}^{0.6} f(x) \, dx = \int_{0.5}^{0.6} 2x \, dx = \left[ x^2 \right]^{0.6}_{0.5} = 0.6^2-0.5^2 = 0.11 \]
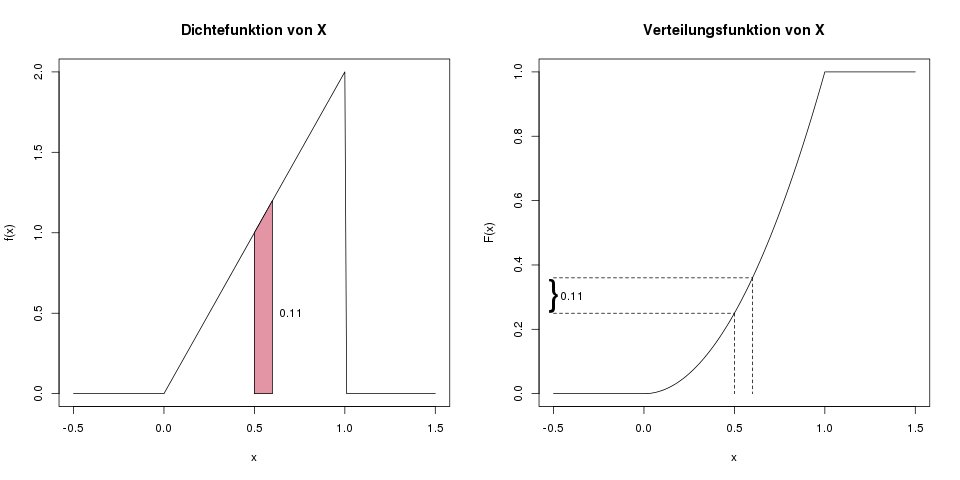
Die grafische Idee hinter der Bestimmung von \(\mathbb{P}(0.5 \leq X \leq 0.6)\). Im linken Bild die Motivation über die Fläche unter der Dichte in diesem Bereich, also die Lösung über das Integral von 0.5 bis 0.6. Im rechten Bild die Motivation über die Verteilungsfunktion, also die Lösung über \(F(0.6)-F(0.5)\).

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Für die Wahrscheinlichkeit, dass X zwischen zwei Werten, z.B. zwischen 0.5 und 1.5 liegt, wurde gesagt, dass:
P(0.5 <= X <= 1.5) = P(X <= 1.5) – P(X <= 0.5) = F(1.5) – F(0.5) ist. Aber verlieren wir dabei nicht P(X=0.5), also ist nicht eigentlich P(X <= 1.5) – P(X <= 0.5) = P(0.5 < X <= 1.5)? D.h. wir müssten hier noch die Dichtefunktion für 0.5 hinzuaddieren?
Viele Grüße
Hi Lukas,
wenn es um diskrete Zufallsvariablen gehen würde, hättest du Recht 🙂
Aber bei stetigen Zufallsvariablen kann man die Dichte nicht einfach hinzuaddieren (dann käme man auch sehr schnell auf Wahrscheinlichkeiten größer als 1).
Bei stetigen Zufallsvariablen bedeutet die Dichte bei 0.5, also f(0.5) nicht dasselbe wie „Die Wahrscheinlichkeit dass das Ergebnis 0.5 ist“. Das (also, die Wahrscheinlichkeit dass das Ergebnis exakt 0.5 ist) ist bei stetigen Zufallsvariablen nämlich 0.
Deswegen ist mathematisch auch P(0.5 <= X <= 1.5) und P(0.5 < X < 1.5) der gleiche Wert. Ich hoffe das klärt es ein bisschen auf. Das ist ein bisschen verwirrend, ich weiß 🙂
Hi, super Artikel! Ich habe eine Frage: Wenn man die echte Dichte feststellen will, wieso lautet die Stammfunktion 2 x 0,5 x^2? Bei 2x dachte ich lautet die Stammfunktion: nur x^2 + C
Danke für Deine Hilfe 🙂
Jo, 2 * 0.5 * x^2 ist dasselbe wie x^2 🙂 Ich habs nur in ausführlich hingeschrieben.
Hallo
Von mir ebenfalls vielen Dank für die tolle Erklärung. Was mir nicht nahe kommt ist im Beispiel die Berechnung für die Verteilungsfunktion. Wann sind die Grenzen von „- unendlich“ bis „x“ und wann kann werden die Intervalle eingesetzt? Ich hatte nämlich gedacht dass Teil 1: „- unendlich bis 0“ Teil 2: „0 bis 1“ und Teil 3: „1 bis + unendlich“ lauten. Und in der Erklärung steht auch, wenn man die Verteilungsfunktion zwischen einem Intervall haben möchte, dass man dann an die Stelle von der oberen Grenze x, die Intervalle einsetzt. Wo ist mein Verständnisfehler? Liebe Grüße und vielen Dank <3
Hallo,
der Unterschied ist:
– Die Verteilungsfunktion F(x) ist definiert als \(\int_{-\infty}^x f(t) dt\), da geht es also bei \(\infty\) los, egal wie sie aussieht. Bei der Normalverteilung ist es z.B. auch so.
– Nur bei so stückweise definierten Dichtefunktionen, so wie bei der beispielhaften hier in der Aufgabe, muss man beim Berechnen des Erwartungswerts usw. stückweise vorgehen, da f(x) ja auch stückweise definiert ist.
Das ist etwas schwer in Worten auszudrücken, leider. Die Erleuchtung kommt aber meist nach dem Rechnen einiger Aufgaben (mit Musterlösung idealerweise)
Viele Grüße
Alex
Vielen Dank Alex, ich rechne das nochmal durch, hoffentlich kommt die Erleuchtung. Ich denke aber ich weiß was du meinst!
Danke für deine schnelle Antwort. Ist eine tolle Seite.
LIebe Grüße Anuschka
Wie kommt man auf diesen Erwartungswert -.-
Ich dachte, wenn alles wegfällt, dann bleibt nur noch das Integral von 0-1 und da kam ja 1 raus wieso ist dann beim Erwartungswert 2/3? Habe irgendwie ein Denkfehler
Hi,
sorry für die späte Antwort, aber vielleicht hilft es ja noch: Das Integral ist hier nicht von f(x), dann wäre die Lösung 1.
Aber es ist x * f(x).
Vielen Dank für die guten Erklärungen hier!
Kürzlich bin ich allerdings im Rahmen des Durchstöberns von Preisbereitschaftsmessungen auf diese Methode gestoßen. Hierbei wird ein optimaler Preispunkt und am Ende der Seite eine Dichtefunktion für diesen Preis generiert.
https://de.linkedin.com/pulse/open-source-der-marktforschung-dirk-obermeier
Meine Fräge wäre, ob ich auch für eine solche sehr asymmetrische Dichtefunktion ein Quantil bestimmen kann. Brauche ich dafür Tabellen? Oder kann ich diese Dichtefunktion überhaupt richtig formelmäßig darstellen?
Ziel wäre es dann z.B. einen Wert definieren zu können, bei dem die Wahrscheinlichkeit, dass er unterschritten wird nur ein vorher definierter Prozentsatz ist.
Vielen Dank im Voraus.
Hi,
das ist keine Dichte aus der Stochastik, die mit einer einfachen Formel dargestellt werden kann, sondern eine empirische Dichte, also aus Daten gewonnen.
Dafür gibt es natürlich auch Quantile. Das sind dann wieder die empirischen Quantile. Einen Artikel dazu findest du hier: http://www.crashkurs-statistik.de/quantile/
Aus der empirischen Dichtefunktion kann man die nicht wirklich ablesen, aber aus der Verteilungsfunktion ginge es schon besser. Am besten ist natürlich, wenn man die Datenreihe vorliegen hat, dann kann man sie einfach sortieren, und die untersten 20% auswählen, und dort dann den Schnitt vornehmen, für das 20%-Quantil.
Ok vielen Dank für die schnelle Antwort.
Im Endeffekt brauche ich also die Dichtefunktion gar nicht.
Wenn ich es richtig verstanden habe gibt mir also das 20%-Quantil den Preis an (z.B. 250) der nur mit einer Wahrscheinlichkeit von 20% unterschritten wird. Das entspräche dann dem Integral der Dichtefunktion von minus unendlich bis 250, wobei ich als Ergebnis 0,2 bekomme.
Ich kann dann sagen, dass das Risiko einer Unterschreitung des Preises von 250 genau 20% beträgt?
Das ist alles richtig, bis auf ein Detail:
Das Risiko einer Unterschreitung beträgt in deinen Daten 20%. Das heißt nicht zwangsläufig, dass das Risiko in der Realität auch genau 20% ist. Durch zufällige Schwankungen in deiner Stichprobe gibt es da immer Unterschiede.
Danke.
Ja das stimmt natürlich. Das ist aber ja glaube ich grundsätzlich bei allen Risikomaßen so. Da hilft dann nur eine größere Stichprobe und das Bootstrapping-Verfahren sollte ja auch eine bessere Prognose ermöglichen.
Ich werde die Seite auf jeden Fall weiterempfehlen 🙂
Wenn ich, um die Varianz zu berechnen, den Verscheibungssatz anwende, muss ich also quasi nur ein x^2 vor die Formel setzen?
Vor das Integral für E(X^2), ja. Um die Varianz dann zu erhalten, fehlen aber noch ein paar Schritte.
Hallo zusammen,
die Erläuterungen sind wirklich klasse – vielen Dank!
Ich habe aber eine Frage zum Integrieren von der Dichte zur Verteilungsfunktion.
Muss ich nicht noch zusätzlich +C ausrechnen (über y=m*x+b oder ähnlich).
Oder kann ich das hier nicht bzw. kann ich das auch weglassen?
Danke und liebe Grüße
Jana
Hi Jana,
die Konstante \(C\) musst du nur addieren wenn es um ein unbestimmtes Integral geht, also wenn die Grenzen nicht angegeben sind.
Bei uns geht es nur um bestimmte Integrale, die Grenzen sind immer mit angegeben (auch wenn es mal z.B. \(-\infty\) sein kann.
Ich sollte das im Artikel vielleicht ausführlicher beschreiben. Demnächst. 🙂
Hier ist aber auch eine gute Erklärung dazu: https://de.serlo.org/mathe/funktionen/stammfunktion-integral-flaechenberechnung/integrale/bestimmtes-unbestimmtes-integral
Viele Grüße,
Alex
Danke für den tollen Artikel!
Was mir mein Statistik – Professor in 3 Monaten nicht beibringen konnte, hast du in einem Artikel geschafft. Vielen Danke dafür, jetzt sehe ich nicht mehr ganz so Schwarz für meine Klausur am Donnerstag 😀
Beim letzten Satz beim Abschnitt „Varianz und Standardabweichung“ ist ein kleiner Tippfehler.
Behoben. Vielen Dank! 🙂