In diesem Artikel wird nun – aufbauend auf das einführende Beispiel – beschrieben, wie man die Regressionsgerade für unsere Beispieldaten berechnet und einzeichnet. Zur Wiederholung:
Wir möchten die Ringgröße (\(y\)) unserer Freundin schätzen, um sie mit einem Ring zu überraschen. Wir wissen aber nur ihre Körpergröße (\(x\)). Um nun die Ringgröße zu schätzen, sammeln wir 10 Datenpunkte von Freunden und Bekannten, und notieren ihre Körpergröße und Ringgröße:
| Person \(i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Körpergröße \(x\) | 156.3 | 158.9 | 160.8 | 179.6 | 156.6 | 165.1 | 165.9 | 156.7 | 167.8 | 160.8 |
| Ringgröße \(y\) | 47.1 | 46.8 | 49.3 | 53.2 | 47.7 | 49.0 | 50.6 | 47.1 | 51.7 | 47.8 |
Wir nennen hier \(y\) die Zielgröße, da ihre Vorhersage unser Ziel ist. Die Körpergröße \(x\) wird allgemein auch Einflussgröße genannt. Es gibt aber noch unzählige andere Namen für die beiden Typen von Variablen. In anderen Quellen wird \(y\) auch häufig Zielvariable, Regressand, Outcome, erklärte Variable oder abhängige Variable (weil sie von \(x\) abhängig ist) genannt. Andere Namen für \(x\) sind Kovariable, Input, Regressor, erklärende Variable oder unabhängige Variable.
Diese Daten können wir nun in ein Streudiagramm einzeichnen, und erkennen sofort, dass größere Frauen tendenziell auch größere Ringe brauchen:
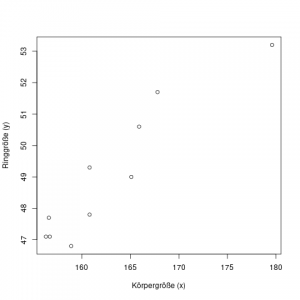
Die Regression ist nun eine statistische Methode, um die bestmögliche Gerade zu finden, die man durch diese Daten legen kann. Eine Gerade wird ja definiert durch zwei Parameter \(a\) und \(b\); man kann sie dann darstellen als
\[ y = a + b \cdot x \]
Manchmal sieht man übrigens statt \(a + b \cdot x\) auch \(\alpha + \beta \cdot x\) oder \(\beta_0 + \beta_1 \cdot x\), aber das sind nur andere Namen für dieselben Zahlen.
Berechnung der Parameter \(a\) und \(b\)
Wenn wir also die bestmögliche Gerade finden wollen, die wir durch diese Punktwolke an Daten legen können, ist das gleichbedeutend damit, dass wir die bestmöglichen Werte für \(a\) und \(b\) finden wollen. Und dafür wurden die folgenden beiden Formeln entdeckt:
\[ b = \frac{\sum_{i=1}^n (x_i – \bar{x}) \cdot (y_i – \bar{y})}{\sum_{i=1}^n (x_i – \bar{x})^2} \]
Die Formel für \(a\) ist einfacher, aber wir müssen vorher das Ergebnis für \(b\) berechnen und dort einsetzen:
\[ a = \bar{y} – b\cdot \bar{x} \]
Die Werte \(\bar{x}\) und \(\bar{y}\) sind jeweils die Mittelwerte der gemessenen Daten \(x\) und \(y\).
Eine kürzere Formel für die Berechnung von \(b\)
Die Formel für \(b\) ist recht chaotisch, aber es gibt eine Möglichkeit, sie kürzer darzustellen, während sie immernoch dasselbe Ergebnis liefert:
\[ b = r_{xy} \cdot \frac{s_y}{s_x} \]
Dabei ist \(r_{xy}\) die Pearson-Korrelation zwischen \(x\) und \(y\), und \(s_x\) und \(s_y\) jeweils die Standardabweichung von \(x\) bzw. \(y\). Diese Werte muss man natürlich auch erstmal ausrechnen, so dass diese kürzere Formel insgesamt wahrscheinlich mehr Rechenaufwand bedeutet – außer man hat diese Zwischenergebnisse schon z.B. in einer vorherigen Teilaufgabe der Klausur erhalten und kann sie einfach einsetzen.
Beispielaufgabe
Wir berechnen hier die Werte \(a\) und \(b\) für die obenstehende Tabelle von 10 Personen. Dazu brauchen wir die Mittelwerte von \(x\) und \(y\) als Zwischenergebnisse:
\[ \begin{align*} \bar{x} &= \frac{1}{10} \cdot (156.3+158.9+160.8+179.6+156.6+165.1+165.9+156.7+167.8+160.8) \\ &= \frac{1}{10} \cdot 1628.5 \\ &= 162.85 \end{align*} \]
Genauso erhält man dann auch
\[ \bar{y} = 49.03 \]
Zum Berechnen von \(b\) könnte man nun sofort loslegen, alles in den Taschenrechner einzutippen. Das ist aber anfällig für Leichtsinnsfehler, und oft reicht auch der Platz im Taschenrechner nicht für diese große Formel aus. Ich schlage also vor, in mehreren Schritten vorzugehen:
Bestimmen der Werte \((x_i-\bar{x})\) und \((y_i-\bar{y})\)
Zuerst brauchen wir Zwischenergebnisse, wo wir von jedem Wert den zugehörigen Mittelwert abziehen. Aus der Tabelle
| Person \(i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Körpergröße \(x\) | 156.3 | 158.9 | 160.8 | 179.6 | 156.6 | 165.1 | 165.9 | 156.7 | 167.8 | 160.8 |
| Ringgröße \(y\) | 47.1 | 46.8 | 49.3 | 53.2 | 47.7 | 49.0 | 50.6 | 47.1 | 51.7 | 47.8 |
werden also die folgenden Werte berechnet:
| Person \(i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \((x_i-\bar{x})\) | -6.55 | -3.95 | -2.05 | 16.75 | -6.25 | 2.25 | 3.05 | -6.15 | 4.95 | -2.05 |
| \((y_i-\bar{y})\) | -1.93 | -2.23 | 0.27 | 4.17 | -1.33 | -0.03 | 1.57 | -1.93 | 2.67 | -1.23 |
Als Beispiel: Der erste Wert für \((x_i-\bar{x})\) ist einfach \(156.3 – 162.85 = – 6.55\).
Berechnen von \(b\)
Jetzt sind wir nicht weit vom Ergebnis entfernt. Wir brauchen im Zähler der Formel für \(b\) nun für jede Person \(i\) das Produkt der beiden Werte \((x_i-\bar{x})\) und \((y_i-\bar{y})\), für die erste Person also z.B. \((-6.55 \cdot -1.93) = 12.6415\).
Im Nenner der Formel für \(b\) brauchen wir das Quadrat der zweiten Zeile, also wir müssen \((x_i-\bar{x})^2\) berechnen.
Diese Werte berechnen wir nun für alle 10 Personen und können sie (ich runde auf zwei Nachkommastellen) in zwei neue Zeilen der Tabelle einfügen:
| Person \(i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \((x_i-\bar{x})\) | -6.55 | -3.95 | -2.05 | 16.75 | -6.25 | 2.25 | 3.05 | -6.15 | 4.95 | -2.05 |
| \((y_i-\bar{y})\) | -1.93 | -2.23 | 0.27 | 4.17 | -1.33 | -0.03 | 1.57 | -1.93 | 2.67 | -1.23 |
| \((x_i-\bar{x}) \cdot (y_i-\bar{y})\) | 12.64 | 8.81 | -0.55 | 69.85 | 8.31 | -0.07 | 4.79 | 11.87 | 13.22 | 2.52 |
| \((x_i-\bar{x})^2\) | 42.90 | 15.60 | 4.20 | 280.56 | 39.06 | 5.06 | 9.30 | 37.82 | 24.50 | 4.20 |
Und wenn man sich jetzt nochmal die Formel für \(b\) anschaut, sieht man dass wir soweit sind: der Zähler ist die Summe der Werte in der dritten Zeile, und der Nenner die Summe der Werte in der vierten Zeile. Die ergeben sich zu
\[ \sum_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y}) = 131.39 \]
und
\[ \sum_{i=1}^n (x_i-\bar{x})^2 = 463.2 \]
Somit können wir also \(b\) berechnen:
\[ b =\frac{\sum_{i=1}^n (x_i – \bar{x}) \cdot (y_i – \bar{y})}{\sum_{i=1}^n (x_i – \bar{x})^2} = \frac{131.39}{463.2} = 0.2836 \]
Berechnen von \(a\)
Der Wert \(a\) ist nun mit diesem Ergebnis ganz einfach zu erhalten:
\[ a = \bar{y} – b\cdot \bar{x} = 49.03 – 0.2836 \cdot 162.85 = 2.8457 \]
Einzeichnen der Regressionsgerade
Wir haben also nun die letztendliche Regressionsgerade berechnen können:
\[ y = 2.8457 + 0.2836 \cdot x \]
Um die Gerade dann einzuzeichnen, reicht es, zwei Punkte zu bestimmen, indem wir irgendwelche \(x\)-Werte aussuchen, und die zugehörigen \(y\)-Werte bestimmen. Die \(x\)-Werte sollten sich im Rahmen der „normalen“ Werte der Daten bewegen. Mit Hilfe der Grafik können wir z.B. \(x=160\) und \(x=170\) aussuchen. Dann berechnen wir mit der Formel der Regressionsgeraden die zugehörigen \(y\)-Werte:
\[ 2.8457 + 0.2836 \cdot 160 = 48.22 \]
\[ 2.8457 + 0.2836 \cdot 170 = 51.06 \]
Die Punkte \((160, 48.22)\) und \((170, 51.06)\) können wir nun in das Streudiagramm einzeichnen, und eine Gerade durch die beiden Punkte ziehen:
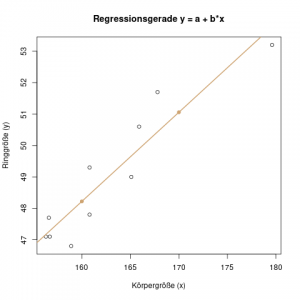
Vorhersage bei der einfachen linearen Regression
Bisher haben wir gelernt, wie man die beiden Koeffizienten \(a\) und \(b\) berechnet. Jetzt möchten wir mit Hilfe der Parameter auch für neue Daten \(x\) vorhersagen, welchen Wert für \(y\) wir erwarten.
Das Ziel, das wir mit der Regression erreichen wollen, ist nämlich folgendes: Angenommen es kommt eine neue Person, von der wir nur die Körpergröße \(x=170\) wissen. Was ist dann der Erwartungswert der Ringgröße \(y\)? Wir suchen also \(\mathbb{E}(y|x)\), den bedingten Erwartungswert von \(y\), gegeben man kennt \(x\).
Bei der einfachen linearen Regression gibt es ja nur eine Einflussgröße \(x\). Die Regressionsgerade lautet also
\[ y = a + b\cdot x \]
Um eine Vorhersage für die Zielgröße \(y\) zu erhalten, müssen wir also einfach den zugehörigen Wert für \(x\) in die Gleichung einsetzen. Die Werte für \(a\) und \(b\) haben wir vorher schon berechnet.
Als Beispiel: Im Beispiel aus dem vorherigen Artikel haben wir die Werte \(a=2.8457\) und \(b=0.2836\) bestimmt. Welche Ringgröße ist nun bei deiner Freundin zu erwarten, wenn sie eine Körpergröße von \(x=\)170cm hat? Dafür berechnen wir:
\[ y = a + b\cdot x = 2.8457 + 0.2836 \cdot 170 = 51.06 \]
Ein Ring mit der Größe 51 sollte also gut bei ihr passen.
Es ist hier noch wichtig zu erwähnen, dass wir nur den Erwartungswert von \(y\) vorhersagen. Die Ringgröße wird also nicht exakt 51.06 sein, sondern es gibt immer einen kleinen Fehler, den man im linearen Modell \(\epsilon\) (sprich: Epsilon) nennt. In Wirklichkeit lautet die Regressionsgleichung also
\[ y = a + b \cdot x + \epsilon \]
wobei \(\epsilon\) einen zufälligen und unbekannten Fehler bezeichnet.
Dieser Fehler heißt meistens Residuum, aber man trifft ihn auch manchmal unter den Namen Fehlerterm oder Epsilon an.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hallo Alex, sehr übersichtliche Zusammenfassung vielen dank dafür.
Was mir gerade in den Sinn kommt. Würden sich nicht jeweils eine Klammer mit (xi – MittelwertX) herauskürzen?
Liebe Grüße
Benjamin
Hi Benjamin,
das darf man hier nicht kürzen, weil es eine Summe ist. Wenn du das Summenzeichen mal evtl. mit einem Beispiel von n=2 ausschreibst, siehst du dass man die Terme nicht kürzen darf.
VG
Alex
Hey Alex,
Super Zusammenfassung, danke dir!
2 Fragen:
Warum teilst du 131,39 nicht durch n (also 10)?
und wieso bei 463,2 ebenfalls nicht durch n?
Weil eigentlich teilt man ja bei der Varianz für das unabhängige Mittel X und bei der Kovarianz von X und Y in beiden Fällen durch N?
Liebe Grüße und ein schönes Wochenende,
Christin
Die beiden 1/10 kann man in dem Bruch rauskürzen. Du kannst alternativ auch beide Zahlen durch 10 teilen, und danach den Bruch ausrechnen (13.139 / 46.32), und dann kommt dasselbe Ergebnis raus 🙂
Erstmal vielen Dank für die super einfach beschriebenen Informationen. In Fachbüchern denk ich mir meistens: Gut, und was bedeutet das jetzt?
Folgende Frage: a und b sind also Regressionsparameter? Oder wird der Begriff für etwas anderes verwendet? Noch mal vielen Dank!
Genau, a und b sind die Parameter, die geschätzt werden.
Hallo Yannick!
„Folgende Frage: a und b sind also Regressionsparameter? Oder wird der Begriff für etwas anderes verwendet?“
Das ist ja eine Frage zu den Begrifflichkeiten, also quasi, was Regressionsparameter eigentlich heißt, wenn ich dich richtig verstehe. Regression bedeutet so viel wie „Rückführung“. Im vorliegenden Fall wird die Ringgröße auf die Körpergröße zurückgeführt. Dabei wird angenommen, dass es einen einfachen linearen Zusammenhang gibt, das Ganze also als eine Gerade dargestellt werden kann. Jede Gerade kann man durch zwei Parameter beschreiben: den Schnittpunkt mit der y-Achse (b) und die Steigung (b). Daher kommt der Name Regressionsparameter. Es kann sich dabei aber auch um mehr als zwei Parameter handeln, wenn es nicht um die einfache lineare Regression geht. Beispielsweise könnte die Ringgröße auch vom Gewicht abhängen, dann würde man das auf eine Ebene im dreidimensionalen Raum zurückführen und braucht dafür 3 Regressionsparameter.
Du hättest mich aber auch direkt fragen können, lieber Arbeitskollege! 😉
Viele Grüße
Hejko
Tolle Erklärung Danke 😀 aber ich habe mal eine Frage ich, bei diesen Daten würde ja jetzt eine Autokorrelation bestehen?
zumindest habe ich mit dem DW-Test die Zahl DW= 3,4 ermitteln könnnen.
Also wird da ja theoretisch die Modellanahme zur Verwendung eines Einfachen Linearen Regressionsanalyse verletzt oder ?
Hallo lieber Alex,
bin totaler Neuling und frage mich
was setzt du den genau für ∑𝑖=1𝑛(𝑥𝑖−𝑥¯)⋅(𝑦𝑖−𝑦¯) und ∑𝑖=1𝑛(𝑥𝑖−𝑥¯)2 um auf das Ergebnis zu kommen?
Mit freundlichen Grüßen
Hi,
zur Schreibweise helfen dir diese Artikel hoffentlich weiter:
https://www.crashkurs-statistik.de/das-summenzeichen-und-rechenregeln/
https://www.crashkurs-statistik.de/lageparameter-mittelwert-median-modus/#mittelwert
Viele Grüße
Alex
Danke sehr gut erklärt schade das man im Studium so eine einführung nicht bekommt 🙂
Hii Alex,
wie müsste ich a und b berechnen, wenn ich z.B y=a+b×x^2 hätte? Kann ich da die Werte quadrieren und in cov-Formel einsetzen und wie bisher rechnen?!
Genau. Wenn deine x-Werte 1, 3, 4 sind, dann ersetze sie einfach durch 1, 9, 16, und rechne mit den Werten die üblichen Formeln aus.
Pingback: Lineare Regression und Anwendung in Python – Statis Quo
Hey Alex, deine Erklärungen sind sehr hilfreich und ich bin sehr dankbar für deine Arbeit.
Es gibt aber noch eine Sache, die mir nicht so ganz klar ist. Der Parameter a ist eigentlich der Y-Achsenabschnitt für x=0. Auf deiner Grafik sieht man das nicht direkt aber wenn die Gerade noch weiter nach links verlaufen würde, dann wäre es der Punkt (0, 2.8457). Die Körpergröße = 0? Verstehe ich das richtig?
Danke
VG
Aleks
Genau 🙂
Danke, jetzt habe Ichs auch kapiert, sehr sehr gut erklärt und vor allem so ausführlich.
Danke!!!
Hey Alex, ich habe so vieles im Internet recherchiert über das Thema und hatte es nie wirklich verstanden, aber dein Blog hat mir super geholfen. Ich habe es nun verstanden *freu*
Hey wirklich guter Blog!
Du rettest viele BWL Studenten damit…werde ich definitiv weiterempfehlen
Wow, vielen Dank für deine so toll verständlichen Beispiele und Formulierungen.
Ich schreibe bald mein Statistik 2 – Klausur. Leider hab ich die ANOVA- Themen auch noch nicht ganz drin, aber deine bisherigen Beiträge, die ich bisher nutzen konnte, sind wirklich Gold wert. 🙂
Weiter so.
Unglaublich gut, was man mit klarer, unprätentiöser Sprache so alles erreichen kann.
Hallo,
also ein wirkllich sehr gelungener Blog. Was 10 skripte zusammn nicht erklären können, schaffst du in 10 Min. Empfehle ich weiter.
Tip Top!
VG
Sebastian
Vielen Dank, lieber Alex, für diese hilfreichen Erklärungen! Ich bestreite meinen gesamten Biometriekurs mit diesem Blog und bin nun zuversichtlich auch die Prüfung zu bestehen 🙂 du erklaerst das einfach super
LG Alice
Hi Alex,
da ich im Verbundstudium nur kurze Infos bekomme wollte ich mich für deinen Post bedanken! Hat mir in etwas mehr als einer Stunde erklärt, was der Dozent in 4 Stunden nicht geschafft hat 😉
Ich wollte mich einfach mal für diese Erklärung bedanken – hat mir sehr geholfen… Danke!
Hi Alex, ich hätte da eine Frage btw.. deine Einträge sind spitze.. aber eine Frage drängt sich mir auf..
Wir haben ja die Y-Werte bestimmt.. mit Y= 48,22 und 51,06. Woher kommen dann auf einmal beim Einzeichnen die Werte 47,64 und 50,44. Vielleicht habe ich auch etwas übersehen?.. Aber das geht mir gerade nicht ein.. Danke
Ohweia, das war ein Fehler von mir. Ich habe da mal die Zahlen verändert, und ganz unten vergessen, sie anzupassen. Die 48.22 und 51.06 sind natürlich richtig, die anderen Zahlen waren falsch. Sorry – ich habs gerade korrigiert.
Danke für den Hinweis 🙂
Alex
Hallo und Dankeschön, das hat mir sehr geholfen! Allerdings habe ich eine Frage zur Kovarianz bzw. zur Berechnung von b. Über dem Bruchstrich steht ja im Prinzip die Kovarianz s(x,y). Muss man diese jetzt nicht noch durch n (also 10) teilen? (Laut manchen Formelsammlungen soll man auch durch n-1 teilen).
Jedenfalls weicht mein Ergebnis für b dadurch um eine Kommastelle von dieser Lösung hier ab.
Sind das einfach verschiedene Annäherungen, oder ein Fehler in meiner Formelsammlung?
Hi,
eigentlich müsste man im Zähler und im Nenner durch n-1 teilen, ja. Da man das aber oben und unten macht, kürzt sich der Faktor wieder raus.
VG,
Alex