Idee
Die Normalverteilung ist aus vielen Gründen die wichtigste Verteilung in der Statistik:
- Modelle (zum Beispiel das lineare Regressionsmodell) mit Normalverteilung sind besonders einfach zu rechnen, da die Formeln zur Bestimmung der Parameter \(\beta\) im Normalverteilungsfall sehr leicht auszuwerten sind.
- Der Durchschnitt einer Stichprobe mit beliebiger Verteilung folgt einer Normalverteilung. Das ist weitaus wichtiger als es beim ersten Mal lesen klingt. Ich kann 100 Zufallszahlen aus irgendeiner Verteilung (stetig oder diskret, auch selbstgebastelte Verteilungen mit irgendeiner Dichte) ziehen, und ihr Mittelwert folgt immer einer Normalverteilung. Dieses Phänomen ist als zentraler Grenzwertsatz bekannt, und wird z.B. beim klassischen \(t\)-Test wichtig. Dort bildet man nämlich einen Stichprobenmittelwert und nutzt aus, dass er annähernd normalverteilt ist.
- Viele natürliche Merkmale folgen einer Normalverteilung. Besonders wenn es ein Merkmal ist, dass aus dem Durchschnitt vieler einzelner Eigenschaften gebildet wird, ist das Resultat am Ende zumindest annähernd normalverteilt. Die Körpergrösse einer Person ist zum Beispiel das Ergebnis (der „Durchschnitt“) vieler verschiedener genetischen Faktoren, und kann für ein gegebenes Geschlecht auch sehr gut mit einer Normalverteilung modelliert werden.
Parameter
Die Glockenkurve der Normalverteilung ist abhängig von zwei Parametern: Dem Mittelwert \(\mu\) und der Varianz \(\sigma^2\). Man notiert eine normalverteilte Zufallsvariable \(X\) als
\[ X \sim \text{N}(\mu, \sigma^2) \]
Mit dem Mittelwert \(\mu\) verschiebt man die Kurve nach links bzw. rechts, und mit der Varianz \(\sigma^2\) verändert man die Form der Kurve – also ob sie enger oder weiter ist. Das folgende Bild veranschaulicht den Einfluss der Parameter:
Vorsicht: Der Parameter ist meist die Varianz, also \(\sigma^2\). Beim Rechnen mit der Normalverteilung (zum Beispiel beim Standardisieren der Zufallsvariablen oder bei Hypothesentests) wird oft mit der Standardabweichung \(\sigma\), also der Wurzel der Varianz, gearbeitet. Hier muss man immer genau hinschauen, welche Variante verwendet wird, und gegebenenfalls zwischen den beiden Werten umrechnen.
Träger
Bei jeder Normalverteilung, also egal welche Parameter \(\mu\) und \(\sigma^2\) sie hat, sind theoretisch alle Realisationen aus den positiven und negativen reellen Zahlen möglich. Der Träger einer Normalverteilung ist also
\[ \mathcal{T} = \mathbb{R} \]
Das erscheint vielleicht etwas seltsam, da man die Normalverteilung oft auch dazu verwendet, Dinge wie die Körpergrösse zu modellieren, und es kann ja keine negativen Körpergrössen geben. Man sollte aber zwei Dinge beachten:
- Bei der Modellierung der Körpergrösse wird zum Beispiel eine Normalverteilung mit \(\mu=165\)cm und \(\sigma^2=100\) verwendet. Da liegt die Wahrscheinlichkeit, dass eine Realisation kleiner als 0 herauskommt, bei ungefähr \(2\cdot 10^{-61}\). Diese Zahl ist eine Null, ein Komma, 60 Nullen, und dann erst eine zwei. Das ist so vernachlässigbar klein, dass in der gesamten Geschichte der Menschheit keine Person in diesem Bereich erwartet wird.
- Die Normalverteilung ist natürlich nur ein „gut genug“ passendes Modell, das zur Beschreibung der Körpergrösse verwendet wird. Die wahre Verteilung der Körpergrösse von Menschen sieht anders aus (und hat natürlich nur einen positiven Träger), aber niemand kennt diese Verteilung, und sie lässt sich wohl auch nicht durch eine so einfache Formel hinschreiben. Daher verwendet man bekannte Verteilungen als Approximation. Man sagt, dass eine bestimmte Verteilung gut genug zur Modellierung ist, und nimmt solche, mit denen man besonders einfach rechnen kann.
Erwartungswert
Der Erwartungswert ist direkt der erste Parameter, \(\mu\). Bei einer Normalverteilung mit \(\mu=4\) erwartet man also im Durchschnitt eine Realisation von 4, egal wie groß die Varianz \(\sigma^2\) ist.
Varianz
Die Varianz der Normalverteilung ist der zweite Parameter, \(\sigma^2\). In der Hinsicht ist die Normalverteilung ein Sonderfall, da ihre beiden Parameter direkt der Erwartungswert und die Varianz sind – sehr bequem.
Dichte
Die Dichtefunktion einer normalverteilten Zufallsvariablen \(X\) mit Parametern \(\mu\) und \(\sigma^2\) lautet
\[ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot \exp \left( – \frac{(x-\mu)^2}{2\sigma^2} \right) \]
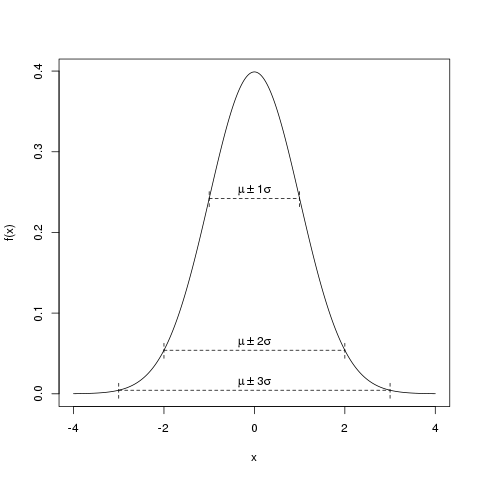
Wenn man sich statt der Varianz \(\sigma^2\) die Standardabweichung \(\sigma\), also \(\sqrt{\sigma^2}\) anschaut, kann man eine beliebige Normalverteilungsdichte skizzieren. Sie hat ihr Maximum an der Stelle \(\mu\), und fällt dann im Bereich von ungefähr \(\pm 3 \sigma\) ab. Außerhalb eines Abstandes von \(3\sigma\) ist die Dichte sehr nahe bei Null.
Verteilungsfunktion
Die Verteilungsfunktion der Normalverteilung kann man nicht mit einer Formel im Taschenrechner berechnen. Das Integral über die Dichtefunktion lässt sich nämlich nicht mit Stift und Papier lösen:
\[ F(x) = \int_{-\infty}^t \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( – \frac{(t-\mu)^2}{2\sigma^2} \right) dt \]
Man nimmt daher eine Verteilungstabelle her, die man häufig am Ende von Statistikbüchern, oder in der Anlage zu Klausuren findet. Wie man die abliest, wird im entsprechenden Artikel erklärt.
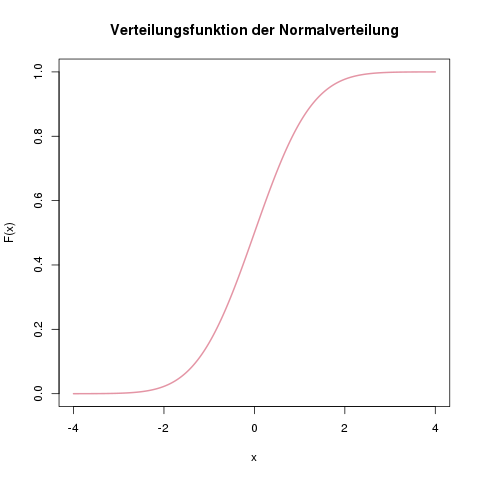
Verteilungsfunktion \(\Phi(z)\) der Standardnormalverteilung (also mit \(\mu=0\) und \(\sigma^2=1\)).
Zum Ablesen von Verteilungstabellen
Nun hat man das Problem, dass es unendlich viele Normalverteilungen gibt, mit jeweils unterschiedlichen Parametern \(\mu\) und \(\sigma^2\). Man bräuchte also eine Tabelle für die Verteilung \(\text{N}(10, 1)\), eine für \(\text{N}(10, 1.4)\), und so weiter. Man hilft sich hier dadurch, indem man nur eine Tabelle verwendet, und zwar für die Standardnormalverteilung, also \(X\sim \text{N}(0,1)\), mit \(\mu=0\) und \(\sigma^2=1\). Nun kann man eine beliebige Normalverteilung standardisieren, und dann deren Wert anhand der Verteilungstabelle bestimmen.
Standardisieren von normalverteilten Zufallsvariablen
Angenommen, wir haben eine Zufallsvariable \(X\sim \text{N}(4, 1)\), und möchten ihre Verteilungsfunktion an der Stelle \(x=3\) wissen. Wir suchen also die Wahrscheinlichkeit, dass diese Zufallsvariable einen Wert kleiner oder gleich 3 erhält. Man muss sich jetzt klar darüber werden, dass das genau dasselbe ist, wie wenn ich für eine Zufallsvariable \(Z\sim \text{N}(0,1)\) die Verteilungsfunktion an der Stelle \(x=-1\) suche. Das folgende Bild veranschaulicht die Gleichheit der beiden Werte anhand der Fläche unter der Dichte:
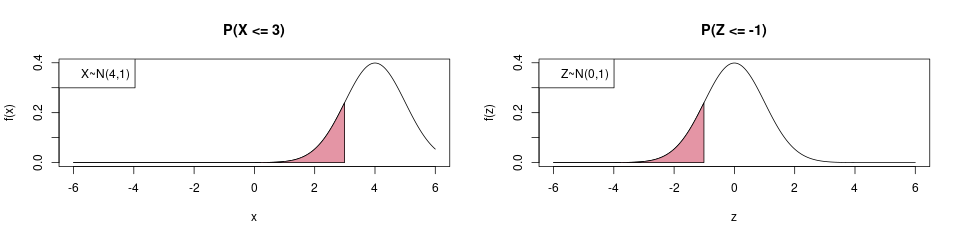
Die linke Fläche, d.h. \(\mathbb{P}(X \leq 3)\) für die Zufallsvariable \(X\sim \text{N}(4, 1)\) ist genau gleich der Fläche \(\mathbb{P}(Z \leq -1)\) für die Standardnormalverteilung \(Z\sim \text{N}(0,1)\).
Man standardisiert eine normalverteilte Zufallsvariable \(X\), indem man also, wie gerade gezeigt, zuerst ihren Mittelwert abzieht, und danach durch die Standardabweichung teilt:
\[ Z = \frac{X-\mu}{\sigma} \]
Das Teilen durch die Standardabweichung streckt bzw. staucht die Glockenkurve so, dass danach ihre Varianz gleich 1 ist.
Damit kann man nun die Verteilungsfunktion jeder beliebigen Normalverteilung bestimmen.
Es gilt also:
\[ \mathbb{P}(X \leq x) = \mathbb{P}(Z \leq \frac{x-\mu}{\sigma}) = \Phi(\frac{x-\mu}{\sigma}) = \Phi(z) \]
Die Standardnormalverteilung wird dabei statt \(F(x)\) mit \(\Phi(z)\) notiert, um Verwechslungen mit der unstandardisierten Verteilungsfunktion zu vermeiden.
Damit können wir nun den oben gesuchten Wert \(\mathbb{P}(X \leq 3)\) für die Zufallsvariable \(X\sim \text{N}(4,1)\) bestimmen:
\[ \mathbb{P}(X \leq 3) = \mathbb{P}(Z \leq \frac{3-4}{1}) = \mathbb{P}(Z \leq -1) = \Phi(-1) = 1 -\Phi(1) = 1 – 0.8413 = 0.1587 \]
Den Wert 0.8413 haben wir dabei mit der Verteilungstabelle bestimmt. Wir mussten die Umrechnung \(\mathbb{P}(Z \leq -1) = 1 -\mathbb{P}(Z \leq 1)\) einführen, da in der Tabelle nur die positiven Werte tabelliert sind. Die Details dazu sind im Artikel zur Verteilungstabelle erklärt.
Der Wert \(F(3)\) der Zufallsvariablen \(X\) ist also gleich dem Wert \(\Phi(-1)\) der standardisierten Zufallsvariable \(Z\). Und da \(\Phi(-1)\) nicht in der Tabelle steht, formen wir es noch um in \(1-\Phi(1)\), und schlagen den Wert für \(\Phi(1)\) nach.
Aufgaben zum Standardisieren
Das Standardisieren muss man einfach einige Male drillen, dann hat man das Prinzip verinnerlicht und Leichtsinnsfehler beseitigt. Bestimme zur Übung die folgenden Werte für verschiedene Normalverteilungen. Beachte, dass der zweite Parameter, \(\sigma^2\), zum Standardisieren noch in die Standardabweichung transformiert werden muss:
- a) Sei \(X\sim \text{N}(2,1)\). Bestimme \(\mathbb{P}(X \leq 3)\).
- b) Sei \(X\sim \text{N}(-1, 4)\). Bestimme \(\mathbb{P}(X \leq 0)\).
- c) Sei \(X\sim \text{N}(0, 5)\). Bestimme \(\mathbb{P}(X > 2)\).
- d) Sei \(X\sim \text{N}(123, 456)\). Bestimme \(\mathbb{P}(X \leq 130)\).
- e) Sei \(X\sim \text{N}(150, 100)\). Bestimme \(\mathbb{P}(160 < X \leq 170)\).
Quantile bestimmen
Das \(\alpha\)-Quantil einer Normalverteilung bestimmt man genau umgekehrt wie den Wert der Verteilungsfunktion:
Man schlägt zuerst das \(\alpha\)-Quantil der Standardnormalverteilung in der Verteilungstabelle nach. Nennen wir es \(z_\alpha\). Man transformiert es nun in das Quantil \(q_\alpha\) der tatsächlichen Normalverteilung, indem man es erst mit \(\sigma\) multipliziert, und dann noch \(\mu\) addiert. Es ist also
\[ q_\alpha = \mu + \sigma \cdot z_\alpha \]
Aufgaben zum Bestimmen von Quantilen
- a) Sei \(X\sim \text{N}(2,1)\). Bestimme das 75%-Quantil \(q_{0.75}\).
- b) Sei \(X\sim \text{N}(-1, 4)\). Bestimme das 50%-Quantil \(q_{0.5}\).
- c) Sei \(X\sim \text{N}(0, 5)\). Bestimme das 97.5%-Quantil \(q_{0.975}\).
- d) Sei \(X\sim \text{N}(123, 456)\). Bestimme das 2.5%-Quantil \(q_{0.025}\).
- e) Sei \(X\sim \text{N}(150, 100)\). Bestimme das 10%-Quantil \(q_{0.1}\).

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!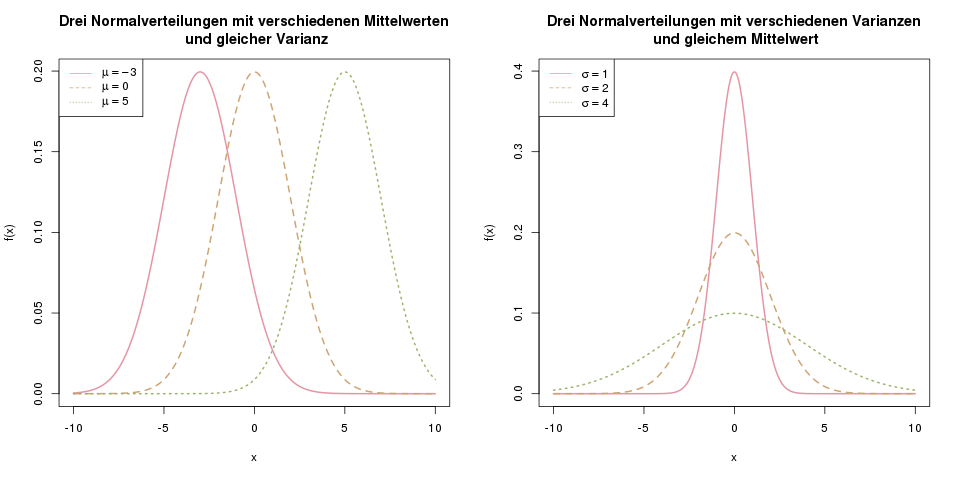
Hi,
ich bin keine Mathematikerin. Daher meine vielleicht „unfachliche“ Frage: Ab welcher „Größe“ kann ich von einer Gauß´schen Normalverteilung ausgehen, d. h. wie viele Vergleichswerte brauche ich. Müssen es 100 sein oder reichen z. B. auch 25?
Vielen Dank vorab!
Oh, Vorsicht! Wenn die Stichprobe nicht normalverteilt ist, dann ist sie es auch bei 100 Beobachtungen nicht. Aber ihr Mittelwert wird zunehmend „normalverteilter“ werden. Die meisten Leute orientieren sich da an 30 Beobachtungen, ab der sie einfach eine Normalverteilung verwenden.
Hi Alex,
erstmal vielen Dank für deinen Blog, ist wirklich super hilfreich in der Klausurvorbereitung !
Ich hab eine Frage zur Standardisierung von Zufallsvariablen : Ist die Standardisierung nur bei normalverteilten Zufallsvariablen möglich? In unserem Skript steht, dass man die Formel zur Standardisierung nutzen kann, wenn es sich um eine ZV mit Erwartungswert μ und Standardabweichung
𝜎 > 0 handelt, aber die könnte ich ja auch von anderen Verteilungen bilden..
Würde mich super über eine Antwort freuen,
LG Anna
Ja, man kann Daten mit beliebigen Verteilungen standardisieren. Manchmal macht das Sinn, wenn z.B. alle Variablen in einem ähnlichen Bereich „leben“ sollen.
Der einzige Unterschied im Spezialfall von normalverteilten Daten ist, dass man dann eben *standard*normalverteilte Daten erhält, d.h. immer noch normalverteilte Daten, aber jetzt mit \(\mu=0\) und \(\sigma=1\).
VG,
Alex
Hallo Alexander,
vorab: Machst sehr stabile Arbeit mit deinem Blog. Habe hiermit nur für meine Klausur gelernt und mein Tutorium bedient sich auch vieler deiner Erklärungen.
Frage: Müsste es bei „Aufgaben zum Bestimmen von Quantilen“ bei Aufgabe a) nicht „q0.75“ statt „q0.25“ sein?
Freundliche Grüße
Khai
Hallo Khai,
ja, da habe ich mich verschrieben. Ist korrigiert, vielen Dank für den Hinweis 🙂
Mann, du machst eine riesige Arbeit. Top!
P.S. du hast minus auf dem Schaubild vom Standardisieren vergessen . P(Z<=-1) statt P(Z<=1)
Oh stimmt, danke. Ich habs gerade korrigiert 🙂
Hammer, vielen vielen Dank!
Beim Standardisieren einer normalverteilten Zufallsvariable hast du bei x=1 das Minus vergessen.
Aber mach weiter so, deine Seite ist wirklich sehr übersichtlich, verständlich und informativ
Oh, richtig! Vielen Dank, ich habs gerade verbessert.
Viele Grüße,
Alex
Dieser Artikel hat mir grad so sehr geholfen, vielen Dank!!! 🙂
Hi, woher weiß ich denn dass es 3SIGMA sind?
Das ist nur eine ungefähre Angabe, keine genaue Regel.
VG,
Alex
Bei der Beispielaufgabe ganz unten a) steht: “ Die Standardabweichung σ ist 10. Die Glockenform fällt also im Bereich vom Mittelwert 175 bis zu ±3σ, also im Intervall [145,195] ab“ .
Müsstes es nicht [145,205] sein?
Ja, richtig. Ich habe es gerade korrigiert – vielen Dank! 🙂