Permutationen

Die Fragestellung in einer Permutation lautet: „Auf wieviele Möglichkeiten kann ich \(N\) Elemente anordnen (oder permutieren)?“ Diese Fragestellung ist im Endeffekt nichts anderes als eine Variation (mit Reihenfolge) ohne Zurücklegen, mit der zusätzlichen Eigenschaft, dass wir aus \(N\) Objekten alle \(N\) ziehen, d.h. \(k=N\).

Die Formel \(\frac{N!}{(N-k)!}\) wird also zu \(\frac{N!}{(N-N)!}\), und damit zu \(\frac{N!}{0!} = N! \).

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Als Beispiel:

• Eine Fußballmannschaft, bestehend aus 11 Spielern, verlässt zu Spielbeginn der Reihe nach die Mannschaftskabine. Wie viele Reihenfolgen sind dabei möglich?

Für die 11 Spieler gibt es \(11! = 39916800\) verschiedene Anordnungen, in der sie aus der Kabine laufen können. So schnell wird ihnen also bestimmt nicht langweilig—falls sie dieses Experiment wirklich durchführen möchten.

Ein weiteres Beispiel ist das Mischen eines Kartenspiels. Bei 52 Karten gibt es \(52!\) verschiedene Reihenfolgen für die Karten. Diese Zahl ausgerechnet ist eine 8 mit 67 Nullen hintendran!

Falls Elemente in der Ausgangsmenge identisch sind

Manchmal besteht eine Grundgesamtheit aus Elementen, die nicht alle voneinander verschieden sind. Betrachten wir den Inhalt eines typischen Studentengeldbeutels:

• eine 2€-Münze
• zwei 1€-Münzen
• eine 50ct-Münze
• drei 10ct-Münzen

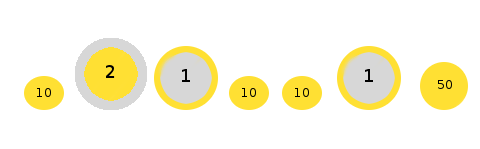
Wieviele Möglichkeiten gibt es, 7 Elemente in eine Reihenfolge zu bringen, wenn einige Elemente davon nicht unterscheidbar sind?

Man möchte jetzt wissen, wieviele Möglichkeiten es gibt, diese \(N=7\) Münzen in eine Reihe zu legen. Dabei sollen die gleichen Elemente—also die beiden 1€-Münzen und die drei 10ct-Münzen—nicht unterscheidbar sein. Man teilt die bekannte Formel \(N! \) durch das Produkt der Fakultäten der Häufigkeiten jedes Elementes. In unserem Fall gibt es also
\[ \frac{7!}{1!\cdot 2!\cdot 1!\cdot 3!} = 420 \] Möglichkeiten, eine Münzreihe zu bilden. Da \(1!=1\) ist, kann man die Einser weglassen und schreibt im Normalfall nur die Fakultäten über 1 in den Nenner:
\[ \frac{7!}{2!\cdot 3!} = 420 \]

Das macht Sinn, da es \(3! \) Möglichkeiten gibt, die drei 10ct-Münzen zu permutieren, und \(2! \) Möglichkeiten für die beiden 1€-Münzen. Diese uninteressanten Möglichkeiten werden im Nenner wieder „herausdividiert“.