Darstellung und Eigenschaften von diskreten Zufallsvariablen

Dieser Artikel beschreibt Eigenschaften, die allen Zufallsvariablen mit diskreten Verteilungen zugrunde liegen. Für Eigenschaften spezieller Verteilungen, z.B. der Poissonverteilung, verweise ich auf den Abschnitt „Verteilungen“ im Inhaltsverzeichnis.

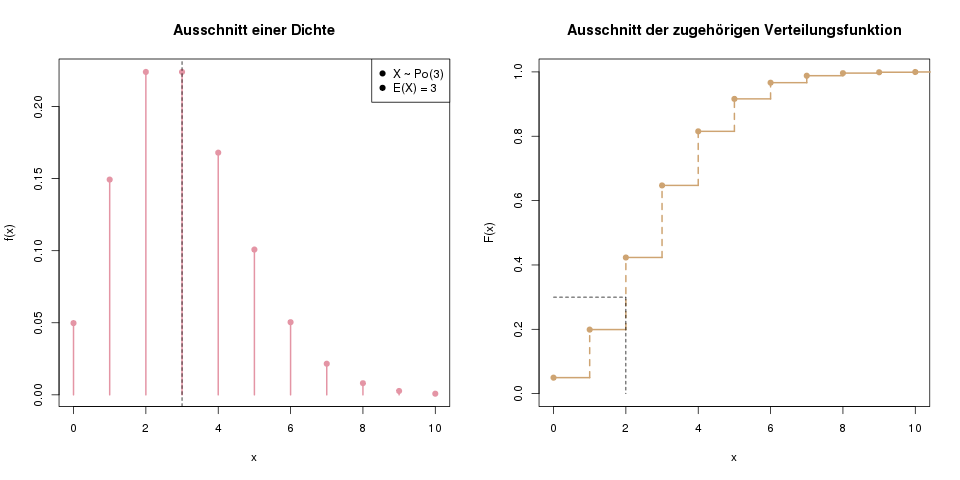
Im linken Bild sieht man die Dichte einer diskreten Zufallsvariable. Man sieht, dass die Wahrscheinlichkeit f(x) für die Ergebnisse 2 und 3 am höchsten ist. Der Erwartungswert E(X) ist 3, und ist mit einer gestrichelten Linie eingezeichnet. Im rechten Bild sieht man die entsprechende Verteilungsfunktion derselben Zufallsvariablen. Außerdem ist das 30%-Quantil eingezeichnet. Man bestimmt es, indem man von der y-Achse auf der Höhe des Quantils (bei uns 0.3) waagerecht nach rechts bis zur Verteilungsfunktion geht, und dann das Lot nach unten fällt. Unser 30%-Quantil ist also 2.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Dichte

Eine Zufallsvariable \(X\) beschreibt, wie schon besprochen, ein Zufallsexperiment, bevor es durchgeführt wird. Der Ausgang dieses Experiments ist also noch unklar. Die Dichte beschreibt nun für jedes mögliche Ergebnis \(x\) dessen Wahrscheinlichkeit. Sie wird mathematisch mit \(\mathbb{P}(X=x)\) dargestellt, und weil das aufwändig zu schreiben ist, mit \(f(x)\) abgekürzt.

Wir verwenden die Dichte, um Wahrscheinlichkeiten für ein einzelnes, oder mehrere mögliche Ergebnisse zu berechnen.

Im Beispiel mit einem Würfelwurf können wir die Dichte wie folgt darstellen:

\[ \begin{align*}f(1) &= \frac{1}{6} \\f(2) &= \frac{1}{6} \\f(3) &= \frac{1}{6} \\f(4) &= \frac{1}{6} \\f(5) &= \frac{1}{6} \\f(6) &= \frac{1}{6} \end{align*} \]

Das geht natürlich auch kürzer. Äquivalent können wir schreiben:

\[ f(x) = \frac{1}{6}, \;\; \text{falls} \; x \in \{ 1,2,3,4,5,6 \} \]

Hiermit können wir z.B. die Wahrscheinlichkeit ablesen, dass wir eine 4 würfeln:

\[ \mathbb{P}(X=4) = f(4) = \frac{1}{6} \]

Außerdem können wir uns mit der Dichte z.B. herleiten, mit welcher Wahrscheinlichkeit wir eine ungerade Zahl würfeln:

\[ \mathbb{P}(X \in \{ 1,3,5\}) = \mathbb{P}(X=1) + \mathbb{P}(X=3) + \mathbb{P}(X=5) = \frac{3}{6} = \frac{1}{2} \]

Damit eine Funktion eine echte Dichte sein kann, muss sie zwei Bedingungen entsprechen:

1. Sie darf nirgends kleiner als Null sein. Es muss also gelten: \(f(x) \geq 0\) für alle \(x \in \mathbb{R}\). Diskrete Dichten sind, wie der Name schon sagt, nur an einigen diskreten Punkten größer als Null, und auf den restlichen reellen Zahlen gleich Null.
2. Die Summe aller ihrer einzelnen Wahrscheinlichkeitswerte muss 1 ergeben. Das macht Sinn, da ja die Wahrscheinlichkeit, dass irgendein beliebiges Ergebnis eintritt, 1 ist.

Verteilungsfunktion

Die Verteilungsfunktion ist eine weitere Variante, eine Zufallsvariable und ihre möglichen Resultate zu beschreiben. Sie drückt aus, mit welcher Wahrscheinlichkeit das Resultat kleiner oder gleich eines bestimmten Werts ist. Die Verteilungsfunktion beschreibt also \(\mathbb{P}(X \leq x)\), und wird mit \(F(x)\) abgekürzt.

Wenn wir die Dichte einer diskreten Zufallsvariablen haben, können wir leicht die Verteilungsfunktion berechnen. Beim Würfelwurf ist z.B.

\[\begin{align*}\mathbb{P}(X\leq 3) = F(3) = f(1) + f(2) + f(3) = \frac{3}{6}\end{align*}\].

Allgemein ist die Verteilungsfunktion definiert als

\[ F(x) = \mathbb{P}(X \leq x) = \sum_{i: x_i \leq x} f(x_i). \]

Der letzte Term beschreibt genau das, was wir im Beispiel zwei Zeilen höher berechnet haben: \(F(x)\) ist die Summe der Wahrscheinlichkeiten aller möglichen Werte \(x_i\), die kleiner oder gleich \(x\) sind. Unter dem Summenzeichen steht der folgende Satz in „mathematisch“ ausgedrückt: „Summiere über alle Werte \(i\), deren zugehöriges \(x_i\) kleiner ist als \(x\)“. In diesem Spezialfall geht \(i\) von 1 bis 6, und die zugehörigen \(x_i\) sind genau dieselben Werte, das muss aber im Allgemeinen nicht so sein – deswegen muss man das allgemeingültig so notieren.

Die komplette Verteilungsfunktion im Spezialfall Würfelwurf ist \(F(x) = \frac{x}{6}\). Somit ist z.B. die Wahrscheinlichkeit, höchstens eine Vier zu würfeln \(F(4) = \frac{4}{6}\).

Quantile

Das Quantil einer Zufallsvariablen ist sehr ähnlich zum empirischen Quantil von bereits gemessenen Daten definiert. So ist etwa das 5%-Quantil einer Zufallsvariable genau der Wert von \(X\), der den Wertebereich so aufteilt, dass \(X\) zu 5% kleiner/gleich diesem Wert ist, und zu 95% größer/gleich. Bei stetigen Zufallsvariablen ist der Wert immer eindeutig, aber bei diskreten Zufallsvariablen kann der Wert ein ganzes Intervall zwischen zwei Ausprägungen annehmen – vergleiche hierzu auch den oben verlinkten Artikel zu empirischen Quantilen.

Allgemein ist ein \(p\)-Quantil so definiert: Das \(p\)-Quantil ist jeder Wert \(x_p\) von \(X\), für den \(F(x_p) = \mathbb{P}(X \leq x_p) \geq p\), und gleichzeitig \(\mathbb{P}(X \geq x_p) \geq 1-p\) gilt.

Erwartungswert

Auch wenn wir nicht wissen, welches Ergebnis unser Zufallsexperiment abwirft, können wir doch berechnen, mit welchem Ergebnis wir „im Mittel“ rechnen können. Wenn wir das Experiment also sehr oft durchführen, und den arithmetischen Mittelwert aller Ergebnisse bilden, erhalten wir den Erwartungswert. Der Erwartungswert für eine Zufallsvariable \(X\) wird mit \(\mathbb{E}(X)\), manchmal auch kurz mit \(\mu\), bezeichnet.

Er lässt sich zum Glück auch von der Dichte berechnen, ohne das Experiment so oft durchführen zu müssen. Dazu summieren wir alle möglichen Ausprägungen, die wir mit ihren zugehörigen Wahrscheinlichkeiten gewichten, auf:

\[ \mathbb{E}(X) = \sum_i x_i f(x_i) \]

Der Erwartungswert der Augenzahl bei einem Würfelwurf ist zum Beispiel \[ \mathbb{E}(X) = 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{6} + 5 \cdot \frac{1}{6} + 6 \cdot \frac{1}{6} = 3.5. \] Hier sieht man auch, dass der Erwartungswert nicht unbedingt eine Zahl sein muss, die auch tatsächlich vorkommen kann. 3.5 Augen werden nie gewürfelt, aber sie sind eben die im Mittel zu erwartende Zahl an Augen.

Bei manchen Verteilungen, wie z.B. der Poissonverteilung, gibt es unendlich viele Ausprägungen, das heisst diese Summe ist unendlich lang. Sie lässt sich aber mit Hilfe eines Tricks (der Exponentialreihe) berechnen und hat ein festes Ergebnis. Meistens steht dieses Ergebnis natürlich in Formelsammlungen und Tabellen und muss nicht von Hand berechnet werden, daher gehe ich hier nicht näher darauf ein.

Varianz und Standardabweichung

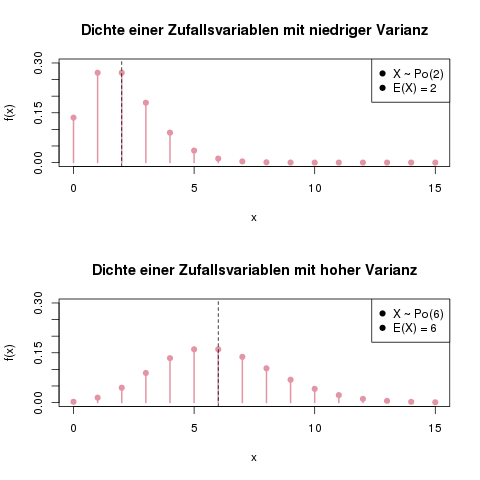
Zwei beispielhafte Dichten. Oben sieht man eine Dichte mit niedriger Varianz, das Ergebnis der Zufallsvariable bewegt sich meist im Bereich von 0 bis 5. Unten eine Zufallsvariable mit höherer Varianz, hier ist die Dichte breit gestreut.

Die Varianz einer Zufallsvariablen wird mit \(\mathbb{V}(X)\), und manchmal kurz mit \(\sigma^2\) notiert. Sie ist die erwartete quadratische Abweichung einer Zufallsvariablen von ihrem Erwartungswert. Die Abweichung vom Erwartungswert \(\mathbb{E}(X)\), nennen wir ihn kurz \(\mu\), ist \(X-\mu\). Die quadratische Abweichung ist \((X-\mu)^2\), und die erwartete quadratische Abweichung ist nun \(\mathbb{E}[(X-\mu)^2]\). Und das ist auch schon die Definition der Varianz einer Zufallsvariablen:

\[ \mathbb{V}(X) = \mathbb{E}[(X-\mu)^2] \]

Dies ist nun ein Erwartungswert einer transformierten Zufallsvariable, und mit der entsprechenden Rechenregel können wir die Varianz so formulieren und berechnen:

\[ \mathbb{V}(X) = \mathbb{E}[(X-\mu)^2] = \sum_i (x_i – \mu)^2 f(x_i) \]

Auch die Varianz ist für Zufallsvariablen ähnlich definiert wie die Varianz für gemessene Daten. Bei gemessenen Daten wird aber erstens mit dem arithmetischen Mittel \(\bar{x}\) statt dem Erwartungswert \(\mu\) gearbeitet, und zweitens jeder Datenpunkt mit \(\frac{1}{n}\) gewichtet, anstatt wie hier mit \(f(x_i)\). Ansonsten sind die Formeln identisch.

Die Standardabweichung \(\sigma\) ist einfach zu berechnen, sobald man die Varianz hat:

\[ \sigma = \sqrt{\mathbb{V}(X)} \]