Quantile (oder genauer gesagt \(p\)-Quantile) sind Werte, die eine Menge von \(n\) Datenpunkten in zwei Teile spalten, und zwar so, dass mindestens ein Anteil \(p\) kleiner oder gleich dem \(p\)-Quantil ist, und mindestens ein Anteil \(1-p\) größer oder gleich dem \(p\)-Quantil.
Man bezeichnet Quantile entweder durch den Anteil \(p\), oder durch eine Prozentzahl, die allerdings dasselbe aussagen. Ein 0.2-Quantil ist dasselbe wie ein 20%-Quantil.
Wer jetzt aufgepasst hat, dem könnte die Definition vielleicht bekannt vorkommen. Der Median ist nämlich nichts anderes als das 50%-Quantil (oder das 0.5-Quantil). Die Quantile können die Daten jetzt aber nicht nur in zwei gleiche Hälften, sondern beliebig aufteilen. Das 0.2-Quantil etwa teilt die Daten in die niedrigen 20% und die hohen 80%. Hierbei steht das \(p\) für die 20% (also die 0.2), und \(1-p\) sind 0.8, also die verbleibenden 80%.
In manchen Fällen kann man die Daten genau in zwei Anteile \(p\) und \(1-p\) aufteilen, wenn man etwa das 20%-Quantil einer Datenreihe mit 5 Elementen bilden will. Dann ist der untere \(p\)-Anteil—also die unteren 20%—durch das erste Element gegeben, und der obere Anteil durch die restlichen, größten vier Elemente. In diesem Fall kann das 0.2-Quantil jeden Wert zwischen dem ersten und zweiten Element annehmen.
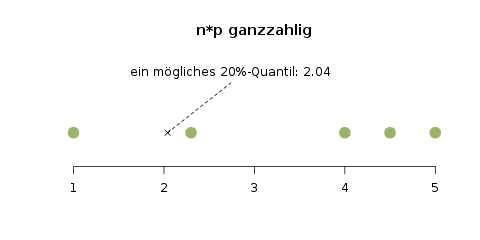
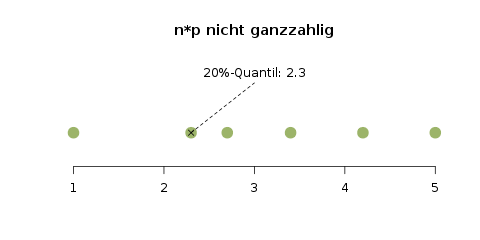
Bestimmung eines 20%-Quantils für die beiden Spezialfälle: Oben ist \(n\cdot p\) ganzzahlig (\(n=5\) Beobachtungen und \(p=0.2\), und das Quantil liegt theoretisch „irgendwo“ zwischen dem ersten und zweiten Punkt. In der Praxis wird meist der Mittelwert zwischen den beiden Punkten genommen. Im unteren Bild ist \(n\cdot p\), also \(6\cdot 0.2\), nicht ganzzahlig, und das Quantil fällt genau auf den zweiten Wert.
Es gibt ein paar verschiedene Methoden, in diesem Fall einen festen Wert für das Quantil zu bestimmen. Meist nimmt man einfach den Mittelwert der beiden anliegenden Punkte. Das haben wir ja beim Median schon so gemacht.
Meistens ist die Situation allerdings ein bisschen anders, und aufgrund der Anzahl der Daten kann man nicht genau einen Anteil \(p\) der Daten abkapseln. Wie bestimmt man zum Beispiel das 20%-Quantil von 6 Daten? Hier merkt man, warum das Quantil so seltsam definiert ist: Wenn wir nämlich das 20%-Quantil als genau das zweite Element festlegen, dann sind \(\frac{2}{6}\), also 33% der Daten kleiner oder gleich diesem Quantil, und \(\frac{5}{6}\), also 83% der Daten größer oder gleich dem Quantil.
Der Spezialfall, in dem man genau einen Anteil \(p\) der Daten bestimmen kann, ist genau dann gegeben, wenn \(n\cdot p\) ganzzahlig ist. In unserem Beispiel mit fünf Datenpunkten und \(p=0.2\) war das der Fall. Die andere Situation, in der wir einen Datenpunkt als Quantil bestimmen, ist gegeben wenn \(n\cdot p\) nicht ganzzahlig ist. Formal wird ein \(p\)-Quantil als \(x_p\) geschrieben, und ist folgendermaßen definiert:
\[ x_p = \begin{cases} \frac{1}{2} (x_{(np)} + x_{(np+1)}) & np \text{ ganzzahlig}\\ x_{(\lfloor np \rfloor +1)} & np \text{ nicht ganzzahlig} \end{cases} \]
Die Klammern \(\lfloor np \rfloor\) bedeuten dabei, dass die Zahl \(np\) auf die nächste ganze Zahl abgerundet wird. Wem das noch ein bisschen kryptisch erscheint, kann ja mit Hilfe der Abbildung oben mal die 20%-Quantile durch diese Formel bestimmen.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hallo Alex,
schöner Artikel, aber wie so oft, wenn es um Quantile geht, scheint er mir zu kurz (übrigens auch in der Wikipedia und vielen, vielen anderen Seiten). Mir ist natürlich bewusst, dass Definitionen im Besonderen unter den vielen Anwendungsgebieten ganz unterschiedlich aussehen.
Wie auch immer…
mMn sollten empirische Quantile (und schon beim Nanen sollte man genau sein um Verwechslungen vorzubeugen) von ordinalen und metrischen Daten unterschieden werden. So ist deine Formel (man bemerke: nicht Definition) für ein Quantil nur für metrische Daten anwendbar.
Die Definition eines emp. Quantils beinhaltet jeweils schwache Ungleichungen, das würde ich noch mit einbauen.
Zuletzt möchte ich anregen, die angegebene Formel für metrische Daten zumindest für den Fall np ganzzahlig anders zu beschreiben. Hier berechnet man nur ein mögliches Quantil. Von „das Quantil“ kann man lediglich bei np nicht ganzzahlig sprechen.
Auf den Spezialfall Median treffen natürlich auch alle Hinweise zu.
Viele Grüße
Patrick
Hi Patrick,
das stimmt natürlich. Hier auf dem Blog habe ich mich aber auf Verständlichkeit konzentriert.
Ich versuche hier, ein intuitives Verständnis für Einsteiger zu schaffen, und auf Aufgaben in Statistikklausuren für Fachfremde zu zielen.
Da leidet natürlich die mathematische Rigorosität manchmal darunter 🙂
Viele Grüße,
Alex
Pingback: Rechnet die Excel-Funktion QUANTIL richtig? – clevercalcul
Hallo, im vorletzten Satz steht, dass np auf die nächste ganze Zahl abgerundet wird. Aber müsste es nicht aufgerundet heißen?
LG und vielen Dank für die tolle Seite.
Nein, da musst du abrunden. Probier es mal mit n=5 aus 🙂
Hallöchen,
kann man Zusammenfassend sagen, wir errechnen mit n*p = xp den „Startpunkt“. Damit meine ike das x, mit welchem wir beginnen. Beispielsweise kommen wir hier auf den Wert 2, so würden wir bei x2 beginnen…
Haben wir dies gefunden, rechnen wir nach der bekannten Formel, welche sich in „ganzzahlig“ & „nicht ganzzahlig“ aufteilt, weiter.
Grundsätzlich brauchen wir Quantile, um die Werte zu teilen und um eben zu wissen, wo die Grenzen der beiden Bereiche liegen.
Ik hoffe das stimmt so 🙂
Beste Grüße,
Felix
Das ist etwas umständlich ausgedrückt, aber ich denke es stimmt so. Wenn es für dich so hilfreich ist, dann bleib bei dieser Betrachtungsweise 🙂
x_p für nicht-ganzzahlige n*p müsste wohl eigentlich mit
x an (n*p-1) abgerundet
berechnet werden und nicht mit
x an (n*p) abgerundet – 1
Hallo,
die beiden Schreibweisen kommen auf dasselbe heraus – da ist egal, ob man vor der 1 oder nach der 1 abrundet 🙂
Aber vorsicht: Die 1 wird addiert, nicht subtrahiert.
VG,
Alex
Hallo, eine dumme Frage: Was genau ist n bei n.p? Vielen Dank! Eine gute Zusammenfassung iat das 🙂
Grüsse
\(n\) ist die Anzahl der Beobachtungen, in den Beispielbildern also 5 oder 6. Ich hab den Artikel gerade ein bisschen ausführlicher gemacht, dass es deutlicher rauskommt 🙂
Hey Alex,
erstmal vielen Dank für deine super Zusammenfassung hier! 🙂
Ich glaube die Reihenfolge hier ist falsch, da du z.b. schreibst „Das haben wir ja beim Median schon so gemacht.“ obwohl erst eine Seite später der Teil zu Lageparametern un Medianen kommt.
Liebe Grüße,
Paul
Hi Paul,
ich hab die Artikel in einer anderen Reihenfolge geschrieben, wie sie im Inhaltsverzeichnis stehen. Daher ist der „nächste“ Artikel unten der mit Lageparametern – aber im Inhaltsverzeichnis steht er davor 🙂
Gruß,
Alex
„und mindestens ein Anteil 1-p größer oder gleich dem p-Quantil.“ Müsste es nicht heißen: „und mindestens ein Anteil 1-p größer oder gleich dem Einser-Komplement des p-Quantils“? Also 1-Q(p)?
Gruß,
Piotr
Hallo Alexander, habe meinen Gedankenfehler inzwischen selber gefunden – bei der Definition des Quantils war mir nicht so ganz klar, ob das die lfd. Nummer des betreffenden Elements ist, oder sein Zahlenwert (der dünne Strich zeigt ja auf die zweite grüne Kugel und nicht deren Zahlenwert (ca. 2,3)). Mit „und mindestens ein Anteil 1-p größer oder gleich dem p-Quantil“ ist also anscheinend gemeint, dass mindestens 80% der Daten einen Wert >= 2,3 haben sollen, so wie auch mindestens 20% der Daten einen Wert <= 2,3 (dieser Zahlenwert damit also zweimal gezählt wird), oder?
Und wenn man die beiden Teilmengen der Stichprobe (die sich also, wie man sieht, auch überschneiden können) mit U und O bezeichnet, müsste man das ganze somit auch wie folgt schreiben können:
U = {x: x <= xp} und |U|>=n*p und O = {x: x >= xp} und |O|>=n*(1-p)Nicht ganz einfach, das Thema…
Gruß, Piotr
Hallo Piotr,
stimmt, da der Pfeil auf den Datenpunkt und nicht die \(x\)-Achse geht, ist das etwas zweideutig. Ich habe die Bilder gerade erneuert, und den Wert des Quantils (2.3 bzw. 2.04) mit in den Text eingefügt. So sollte das klarer sein.
Die beiden Teilmengen können sich überschneiden, genau. Das ist der Fall wenn n*p nicht ganzzahlig ist.
Danke für den Hinweis!
Alex