Histogramme sehen zunächst ähnlich aus wie Balkendiagramme, werden aber für stetige statt diskrete Daten verwendet. Um ein Histogramm zu zeichnen, muss man seine Daten zuerst klassieren, d.h. Gruppen bilden und sie ihnen zuordnen.
Einfacher: Histogramme für gleich breite Gruppen
Am einfachsten sind Histogramme zu zeichnen, wenn diese Gruppen gleich breit sind. Mißt man zum Beispiel die Körpergröße von 20 Personen, könnte man diese Gruppen in 10cm-Abständen bilden, also von 150-159cm, von 160-169cm, und so weiter.
Wir bauen nun ein Histogramm für die folgenden zwanzig Körpergrößen:
| 172 | 164 | 160 | 162 | 173 | 180 | 158 | 185 | 171 | 181 | 162 | 184 | 177 | 175 | 177 | 174 | 158 | 151 | 192 | 177 |
Zuerst müssen wir die Gruppen festlegen, in die wir die Daten zuordnen wollen. Wir zeichnen zuerst ein Histogramm für fünf gleich breite Gruppen:
| Gruppe | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Intervall | [150, 160) | [160, 170) | [170, 180) | [180, 190) | [190, 200) |
Die eckigen und runden Klammern beschreiben die jeweiligen Grenzen des Intervalls. In der zweiten Spalte ist z.B. die 160 enthalten, da davor eine eckige Klammer steht, aber die 170 ist nicht enthalten, da dort eine runde Klammer ist. Wenn also jemand genau 170cm groß ist, fällt er in die dritte Gruppe. Falls jemand 169.8cm groß ist, fällt er in die zweite Gruppe.
Jetzt zählen wir, wie viele Personen in jede Gruppe fallen. Es gibt z.B. drei Personen in der Gruppe von 150 (einschließlich) bis 160 (ausschließlich). Mit diesen Daten könnte man nun schon ein Histogramm mit absoluten Häufigkeiten zeichen. Das möchten wir aber nicht, da diese Art dann bei komplizierteren Histogrammen mit variablen Gruppenbreiten nicht mehr funktioniert (wer mir nicht glaubt, kann es gerne versuchen, das ist eine schöne Übung). Wir berechnen als Höhe der einzelnen Balken stattdessen die Dichte, und zwar wie folgt:
\[ h_i = \frac{n_i}{N \cdot b_i} \]
Hier ist \(h_i\) die Höhe des \(i\)-ten Histogrammbalkens, \(n_i\) ist die Anzahl der Personen in dieser Gruppe \(i\), \(N\) ist die Gesamtzahl an Personen (bei uns \(N=20\)), und \(b_i\) ist die Breite der \(i\)-ten Klasse (bei uns sind alle Klassen gleich breit, also \(b_i=10\) für alle Klassen). In der ersten Klasse ist die Höhe zum Beispiel \(h_1 = \frac{3}{20 \cdot 10} = 0.015\).
Am einfachsten erstellt man all diese Daten in einer Tabelle:
| Gruppe \(i\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Intervall | [150, 160) | [160, 170) | [170, 180) | [180, 190) | [190, 200) |
| Anzahl an Personen in dieser Gruppe, \(n_i\) | 3 | 4 | 8 | 4 | 1 |
| Histogrammhöhe, \(h_i\) | 0.015 | 0.02 | 0.04 | 0.02 | 0.005 |
Damit kann man nun ein Histogramm zeichen:

Das linke Histogramm haben wir gerade berechnet. Das rechte unterscheidet sich nur darin, dass auf der \(y\)-Achse absolute Zahlen verwendet wurden—es wurden also statt den Höhen \(h_i\) die Anzahl an Personen, \(n_i\) gezeichnet. Man sieht hier also direkt, dass in der mittleren Klasse 8 Personen liegen. Aber wie gesagt, für variable Klassenbreiten kann man das dann nicht mehr machen.
Der Anteil an Beobachtungen in jeder Gruppe entspricht nun der Fläche dieser Balken. In der ersten Gruppe ist ein Anteil von \(10\cdot 0.015 = 0.15\), also 15% der Daten, was bei 20 Personen genau 3 Personen entspricht. Diese Art der Interpretation wird wichtig, wenn wir uns Histogramme mit variablen Gruppenbreiten ansehen:
Komplizierter: Histogramme für variable Gruppenbreiten
Diese Art von Histogramm sieht man in der Realität so gut wie nie – zumindest ich bin noch nie einem begegnet. Ich habe aber in einer Klausur mal ein solches Histogramm zeichnen müssen, daher zeige ich hier auch, wie man diese Art erstellt.
Das einzige, was hier noch dazukommt, sind die Klassenbreiten \(b_i\), die ja nun verschieden breit sind. Schauen wir uns ein Histogramm für die folgenden Klassen an:
| Gruppe \(i\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Intervall | [140, 160) | [160, 165) | [165, 190) | [190, 200) |
Mit derselben Formel von oben, in die wir nun aber unterschiedliche Klassenbreiten eintragen, erhalten wir nun diese Werte:
| Gruppe \(i\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Intervall | [140, 160) | [160, 165) | [165, 190) | [190, 200) |
| Klassenbreite \(b_i\) | 20 | 5 | 25 | 10 |
| Anzahl an Personen in dieser Gruppe, \(n_i\) | 3 | 4 | 12 | 1 |
| Histogrammhöhe, \(h_i\) | 0.0075 | 0.04 | 0.024 | 0.005 |
Das zugehörige Histogramm sieht wie folgt aus:
Wie schon gesagt, diese Darstellung macht wenig Sinn, könnte aber in einer Klausur abgefragt werden, um zu prüfen ob man das Prinzip verstanden hat.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!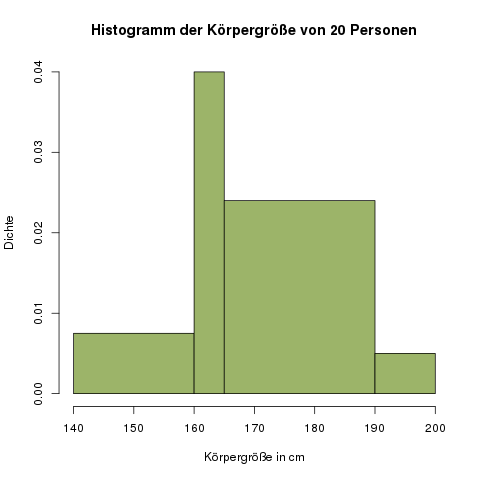
Es kommt in der Praxis tatsächlich häufig vor, dass Daten in gruppiertere Form vorliegen und die Gruppen unterschiedlich breit sind. Bei Sekundärdaten können wir die Klassenbreiten nicht selbst wählen. Dann „macht diese Darstellung Sinn“, auch wenn es nicht den täglichen Sehgewohnheiten entspricht. Leider weden solche Daten häufig falsch graphisch dargestellt (z.B. in Globus-Graphiken). Es ist wichtig, diesen Fehler und den damit verbundenen falschen visuelle Eindruck erkennen zu können. Schon allein deshalb ist es wichtig, Histogramme mit ungleich breiten Klassen gut zu verstehen.
Hallo Alex,
warum funktioniert es nicht, bei unterschiedlichen Klassenbreiten mit den absoluten Häufigkeiten die absoluten Häufigkreitsdichten zu ermitteln?
Wenn ich beispielsweise für die Körpergrösse 2 Klassen habe, einmal von 150-159 cm und einmal von 160-179 cm, und ich teile jeweils die abs. Häufigkeit durch die jeweilige Klassenbreite, hier beispielsweise 5/10=0.5 und 7/20=0.35, dann bedeutet doch beispieslweise der Wert 0.5, dass in der ersten Klasse 0.5 Personen auf 1 cm kommen, was die absolute Häufigkeitsdichte der ersten Klasse wäre.
Sie schreiben, dass man bei unterschiedlichen Klassenbreiten nur mit den relativen Häufigkeiten die relativen Häufigkeitsdichten ausrechnen kann, dass leuchtet mir nicht ein.
mit freundlichen Grüssen
Marvin
Moment, mit „absolut“ meine ich die Anzahl der Personen. Die Dichte nenne ich „relativ“, weil es die Anzahl Personen (bei dir: 5) geteilt durch die Breite des Intervalls (bei dir: 10) ist.
Wir meinen also dasselbe (und damit hast du mit deiner Aussage auch Recht), aber haben nur andere Wörter dafür verwendet 🙂
Ah okey, danke Dir! 🙂
Pingback: t-Verteilung: Stichprobenmittelwerte | Crashkurs Statistik
Na gut.
Wenn Nutzeranalysen und IT Performancestatistiken in Zeiten von immer stärkerer Digitalisierung und steigendem eCommerce für dich so seltene Nischenanwendungen sind, dann stimme ich zu.
„Diese Art von Histogramm sieht man in der Realität so gut wie nie“
Das ist eine ziemlich gewagte Aussage!!
“ – zumindest ich bin noch nie einem begegnet. “
Aha, heißt wohl nur, dass du viele Anwendungen für Histogramme noch nicht gesehen hast, insbesondere wenn eine oder beide äußeren Klassengrenzen offen sind (macht bei Körpergröße natürlich keinen Sinn).
Ein Histogramm mit einer offenen Klassengrenze wäre gar nicht möglich, da die Klassenbreite \(b_i\) für diese Klasse dann unendlich wäre, und die Höhe \(h_i\) dementsprechend Null – egal, wie viele Beobachtungen \(n_i\) in dieser Klasse liegen. Weil: \(n_i / \infty = 0\), für alle \(n_i\).
Außerhalb von Klausuren bin ich, wie gesagt, noch nie einem solchen Histogramm begegnet. Aber ich würde mich über einige Beispiele freuen, die ich hier aufnehmen kann. Hast du da ein paar?
Zur Höhe: Richtig, deswegen gibt es in der Praxis ja „Überlauf-“ oder „Unterlaufcontainer“.
Beispiel?
Hmmm . Latenzdiagramme bei Servercalls über Netzwerke fällt mir spontan ein.
Hier werden m.W.n. meist Klassenbreiten verwendet, die nach oben hin breiter werden, getrieben durch die erwarteten Häufigkeiten, um das Diagramm zu balancieren. Plus Überlauf für Ausreißer, die aus Fehlverarbeitungen resultieren.
Anderes Beispiel für ungleiche Klassen sind demografische Altersauswertungen, wobei die Klassenbildung durch z.B. Marktzielgruppen vorgegeben ist.
Da ist der Teenagerbereich anders geschnittem als das Kindalter, die Erwachsenengruppen und die Seniorenklasse.
Gut, das würde ich jetzt aber in die Schublade ‚Spezialfälle‘ stecken, die ich durch meine Relativierung „so gut wie nie“ abgegriffen habe. 🙂
Es gibt tatsächlich viele Anwendungsfälle für unterschiedlich große Klassenbreiten. Sie machen immer dann sinn, wenn kleinere Einteilung im Gesamtbild zu Ungleichmäßigkeiten führt. So würde ich es Jetzt unwissenschaftlich beschreiben.
Man könnte sogar sehr gut eine größere Klassenbreite für das Beispiel mit den Körpergröße bilden. Die Körpergrößen, die du aufgeführt hast, also von 150 bis 200 cm ist ein mehr oder weniger Durchschnittsbereich. man könnte aber auch (die Einteilung wird jetzt ethisch nicht korrekt sein) einen Bereich von 0 bis 150 cm für kleinwüchsige Erwachsene aufspannen.
Danke, danke! – überlege schon den ganzen Tag und länger, was es mit der Dichtefunktion der Normalverteilung auf sich hat. Mithilfe deiner Grafiken einschließlich der Formel konnte ich es mir erklären. Nebenbei natürlich Histogramme verstanden.
Toll, vielen Dank für die Erläuterung. Die Berechnung der Balkenhöhen bei variabler Breite fehlt in meinem Skript – jetzt verstehe ich auch, was es mit der Flächenproportionalität auf sich hat. ?
Viele Grüße
Silke
Vielen vielen Dank! Habe in 2 Tagen eine SA über u.A. Statistik, und mein Mathematik-Buch hat Histogramme, insbesondere welche mit unterschiedlicher Balken-breite, nur minder erklärt. Das ganze macht jetzt endlich Sinn für mich.
Einen schönen Tag noch 🙂