Ein Boxplot ist eine grafische Zusammenfassung der folgenden fünf Punkte:
- Minimum (= 0%-Quantil)
- 25%-Quantil
- Median (= 50%-Quantil)
- 75%-Quantil
- Maximum (= 100%-Quantil)
Da man das Minimum, den Median und das Maximum als 0%-, 50%- bzw. 100%-Quantil ausdrücken kann, zeigt der Boxplot eigentlich nur fünf häufig verwendete, interessante Quantile. Dabei ist die Box und ihre sogenannten „Whiskers“, die Striche außerhalb der Boxen, wie folgt aufgebaut:
Die Box spannt sich vom 25%-Quantil bis zum 75%-Quantil auf, in ihr ist der Median durch einen Querstrich markiert. Außerhalb der Boxen spannen sich nach oben und unten die Whiskers zum Minimum bzw. Maximum der Datenreihe.
Es gibt eine Ausnahme, in der die Whiskers meistens nicht bis zum Minimum bzw. Maximum gezeichnet werden. „Meistens“, weil dieses Vorgehen nirgends festgelegt ist, und nur eine Art Quasi-Standard ist. Falls die Whiskers länger sind als das 1.5-fache der Box (d.h. der 1.5-fache Interquartilsabstand), werden sie nicht bis zum letzten Punkt gezeichnet, sondern nur bis zum letzten Punkt der weniger als das 1.5-fache des Interquartilsabstands von der Box entfernt ist. Alle Datenpunkte, die dann ausserhalb der Whiskers liegen, werden als Ausreißer separat eingezeichnet.
Am Boxplot kann man auch zwei Streuungsmaße ablesen: Die Spannweite ist nämlich der Abstand zwischen den beiden Whiskers (bzw. zwischen den äußersten Ausreißern). Der Interquartilsabstand, der ja als \(x_{0.75} – x_{0.25}\) definiert wurde, ist genau die Breite der Box.
Beispielaufgabe
Um einen Boxplot von Hand zu zeichnen, benötigen wir nur die sogenannte Fünf-Punkte-Zusammenfassung einer Datenreihe. Diese wollen wir jetzt anhand von Beispieldaten berechnen.
Nehmen wir an, wir bekommen einen Datensatz mit \(n=20\) befragten Autofahrern. Die Personen haben uns gesagt, wie oft sie in ihrem Leben schon geblitzt wurden. Wir bekamen von den Personen die folgenden Antworten:
1 4 3 3 7 1 0 9 2 3 1 1 2 0 5 0 0 1 0 2
Wir brauchen also als allererstes für die Box das 25%- und das 75%-Quantil sowie den Median. Dazu sortieren wir die Liste zuerst:
0 0 0 0 0 1 1 1 1 1 2 2 2 3 3 3 4 5 7 9
Der Median ist für 20 Elemente definiert als \(\frac{1}{2} (x_{(10)} + x_{(11)})\), also 1.5. Die Quantile sind \(x_{0.25} = \frac{1}{2} (x_{(np)} + x_{(np+1)}) = \frac{1}{2} (x_{(5)} + x_{(6)}) = 0.5\), und \(x_{0.75} = 3\). Die Box erstreckt sich also von 0.5 zu 3, mit dem Median-strich bei 1.5.
Für die Whisker müssen wir nachsehen: Das Minimum der Daten ist 0. Der Whisker streckt sich bis zum Minimum, falls es nicht weiter als \(1.5\cdot IQR\) von der Box (also von \(x_{0.25}\)) entfernt ist. \(IQR\) steht hier für interquartile range, also den Interquartilsabstand, oder \(x_{0.75}-x_{0.25}\). Der ist bei uns 2.5. Und das Minimum ist nicht weiter als \(1.5\cdot 2.5\) von 0.5 entfernt: Daher geht der untere Whisker bis zum Minimum 0.
Das Maximum der Daten liegt bei 9. Das ist 9-3=6 von der Box entfernt. Geteilt durch die \(IQR\) ergibt das \(6/2.5 = 2.4\). Das bedeutet, dass das Maximum die 2.4-fache IQR als Abstand zur Box hat, und das ist mehr als das 1.5-fache. Der Whisker geht daher bis zum größten Datenpunkt, der kleiner als \(1.5\cdot IQR\) von der Box entfernt ist. Das wäre bei uns der Punkt, der (von unten) am nähesten an \(3 + 1.5\cdot 2.5\), also 6.75 liegt. Das ist 5; und genau so weit geht unser oberer Whisker. Alle Werte, die darüber liegen (die sogenannten Ausreißer), werden noch als einzelne Punkte eingezeichnet.
Der dazugehörige Boxplot sieht so aus:

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!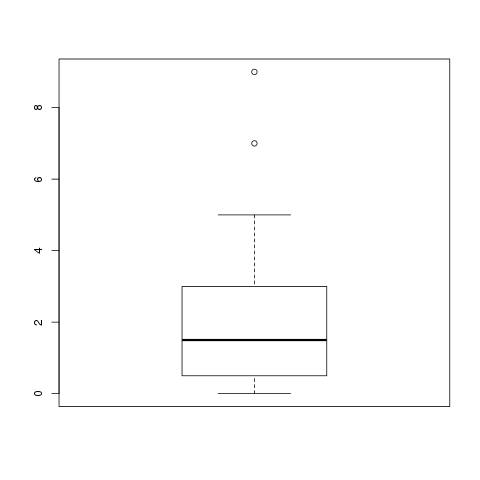
Hey Alex,
Wie ist ein Boxplot zu deuten, bei dem es keine obere Antenne gibt? Der Median liegt zeitgleich am unteren Rand der Box (also ist der Gesamt-Median und der Q1-Median der selbe).
Das obere Ende der Box endet bei dem Wert 5, was der höchst mögliche Wert zur Auswahl (im Rahmen einer Umfrage mit einer Selbsteinschätzung auf einer Skala von 1-5) war. Innerhalb der Box liegen ja immer 50% der Daten, und je 25% darüber bzw. darunter, zumindest im Normalfall.
Es werden aber laut Einstellung in SPSS alle Daten angezeigt. Wie gehe ich nun also mit meiner fehlenden Antenne, also laut Diagramm meinen fehlenden 25% im Rahmen meiner empirischen Analyse um?
Für jede kleine Hilfe wäre ich dir sehr dankbar!
Viele Grüße
Lena
Hi Lena,
das kann passieren wenn du eine sehr kleine Stichprobe hast, oder wenn das 75%-Quantil (also das obere Ende der Box) gleich dem 100%-Quantil (also dem Ende der oberen Antenne) ist.
Du kannst mal selbst einen Boxplot für die Datenreihe 1, 3, 5, 5, 6, 6, 6 zeichnen. Hier ist das 75%-Quantil *und* das 100%-Quantil gleich 6.
VG
Alex
Hey Alex,
ich beschäftige mich gerade mit der Frage, ob ich ein Boxplot auch für gruppierte Daten erstellen kann, also bspw. Für Altergruppen (20-25, 26-30, etc), wenn wirklich nur die Gruppen vorliegen 🙂 Ansich würden dann ja lediglich die Gruppen als Median etc angezeigt werden, aber ist das überhaupt gültig?
Danke schonmal im voraus 🙂
Notfalls kannst du das, ja. Dann wäre es genauso wie ein Boxplot für ordinale Daten (du kannst gruppierte Daten als ordinal betrachten).
Aber ideal wären natürlich die originalen, nicht-gruppierten Daten 🙂
Hallo,
welches Skalenniveau brauche ich denn mindestens um einen Boxplot erstellen zu können?
Bei Wikipedia steht, dass es bereits mit ordinalskalierten Daten geht.
Ich kann mir die Durchführung sehr schlecht vorstellen.
Könntest du mir vielleicht ein Beispiel geben?
Danke und LG,
Lena
Hi Alex!
Ich habe eine Frage, zu der ich noch nirgendwo eine Antwort finden konnte — leider auch nicht in deiner extensiven und äußerst hilfreichen/leicht zu verstehenden Erklärung:
Die Breite hängt bekanntermaßen mit den Quartilen zusammen, aber wodurch wird die zweite Dimension der Box bestimmt? Gibt es ein festes Verhältnis zur Breite o.ä.?
Liebe Grüße und danke für die tolle Arbeit,
Evan
Die zweite Dimension hat beim Standardboxplot keine Information… die Box kann man so breit bzw. so schmal machen wie man möchte 🙂
VG
Alex
Hallo Alex,
gibt es eine Mindestgröße für eine Datenreihe, ab der ein Boxplot Sinn macht, bzw. eine Aussagekraft entwickelt, z.B. n>5 (im Beispliel oben ist n=20) ???
Danke für die tolle Crashkursdarstellung 😉
Hi,
es gibt keine offizielle Mindestgröße, aber da man alle \(n\) Werte auf 5 Zahlen (die Quantile) zusammenfasst, finde ich einen Boxplot unter 10 Werten nicht wirklich sinnvoll. Ab 20 Werten sind die Daten dann auch einigermaßen stabil, so dass man aus dem Boxplot sinnvolle Information lesen kann.
Viele Grüße,
Alex
Danke! Dann wird die Auswertung einer Merkmals von 6 Probanden (Wert y über die Zeit t gemessen) in Form eines Kastendiagramms alias Boxplot wohl relativ sinnfrei sein, vermute ich 😉
Hallo tolle Erklärung!
Bei der Eingabe des Beispiels wird bei mir die Box bei 0,75 gestartet (obwohl das Mittel aus 0 und 1 bekanntlich 0,5 ist).
Gibt es dafür eine Erklärung?
Danke Vorab und viele Grüße
Andre
Hallo,
wo gibst du das Beispiel denn ein?
Es gibt ein paar verschiedene Regeln, Quantile zu bestimmen, die zwischen zwei Zahlen liegen. Manche Programme verwenden da andere Schätzer als den Mittelwert zweier Zahlen. Die sind teilweise recht kompliziert. Schau mal hier unter „type 1“ bis „type 9“:
https://stat.ethz.ch/R-manual/R-devel/library/stats/html/quantile.html
Ich würde je nach Programm herausfinden welcher Algorithmus verwendet wird, und den dann einfach akzeptieren… 🙂
VG,
Alex
Hallo Alex, schnelle Antwort! Danke.
In Excel gibt es die Möglichkeit für ein Boxplot, heißt dort Kastendiagramm.
Auch bei der Berechnung vom 25% Quantil bekomme ich dort 0,75 angezeigt.
Ist dir bekannt, wie das geändert werden kann?
Gruß Andre
Hi Alex,
Was bedeutet es, wenn ich nur die Antenne ohne Box rausbekomme (Excel).
Skala: 1-7
MIN = 5
Q1 = 6
Median = 6
Q3 = 6
MAX = 7
Wenn ich die Zahlen anschaue, ist das für mich logisch (Bauchgefühl), aber ich muss das natürlich im empirischen Teil wissenschaftlich er(klären) können.
Kannst Du mir helfen?
LG,
Alex. (andra)
Naja, die Box geht von Q1 bis Q3. Also in deinem Fall von 6 bis 6. Die „Box“ ist da also nur ein Strich 🙂
Hi.
Ich habe noch eine Frage zur Darstellung von Boxplots. Wenn ich diese für eine Arbeit verwende, muss ich dann die Ausreißer und Extremwerte im Diagramm anzeigen? Oder darf ich diese auch ausblenden (dies würde im Methodenteil natürlich vermerkt)?
Mein Problem ist nämlich, dass ich in meinen Diagrammen zum Teil einzelne Ausreißer habe, die so extrem sind, dass dadurch der Rest meines Diagramms (aufgrund der riesigen Skalierung) uninterpretierbar ist. Da es sich jedoch um vollständig neue und bisher unbekannte Messparameter handelt, möchte ich auch keine Daten löschen, da es nicht klar ist ob es sich um Messfehler oder doch um mögliche (wenn auch extreme) Ausprägungen handelt.
Ich bin für jede Hilfe dankbar.
Viele Grüße
Jocy
Ich denke, wenn du im Methodenteil (und am besten in der Bildunterschrift) erklärst wie der Boxplot gezeichnet wurde, ist das okay. (Ein benotender Betreuer könnte da aber natürlich eine andere Meinung haben).
Bei extremen Ausreißern bietet sich übrigens oft auch eine Transformation der Daten an, z.B. indem du den Logarithmus verwendest.
Viele Grüße,
Alex
Hi,
ist es theoretisch möglich, dass die Ausreißer so gravierend sind, dass sie die Quartilen und den Median derart verändern, dass das tatsächlich auftretende Maximum (abgesehen von Ausreißern) kleiner als die dritte Quartile ist?
Danke im Voraus!
Uff, komplizierte Frage 🙂
Die Antwort lautet „nein“, aber die Erklärung dafür ist ein bisschen aufwändig.
Mit „tatsächliches Maximum abgesehen von Ausreißern“ meinst du das obere Ende des Whiskers, oder? Wenn ja:
Da das dritte Quartil das obere Ende der Box ist, und das obere Ende des Whiskers ja im Falle hoher Ausreißer 1.5*IQR von der Box entfernt ist, ist es dann auch immer weiter weg als das dritte Quartil.
Übrigens: Gravierende Ausreißer verändern den Median nicht. Sie würden nur den arithmetischen Mittelwert verändern.
Viele Grüße,
Alex
Müsste der Obere Whisker dann nicht 6 sein, wenn man den Wert sucht, der von unten am nähesten an 6,75 ist?
Man sucht den Datenpunkt, der von unten am nähesten an 6.75 ist. Da in den Daten keine 6 vorkommt sondern nur eine 5, ist es der. Wenn in den Daten z.B. eine 6.25 vorkommen würde, dann würde man die nehmen.
Viele Grüße,
Alex
Hallo,
ich verstehe leider nicht, wie man auf den Wert 5 für den oberen Whisker kommt.
Wäre es möglich, dies bitte ein wenig genauer zu erklären?
Vielen lieben Dank!
Hi, ich habs jetzt ein bisschen ausführlicher erklärt. Welchen Satz bzw. Teil genau verstehst du denn nicht?