Das Wichtigste in Kürze
Die grundlegende Frage, die durch die Lorenzkurve beantwortet wird, ist die folgende: Welcher Anteil der sortierten Grundgesamtheit besitzt welchen Anteil an der Merkmalssumme?
Um die Kurve zu zeichnen, benötigt man also eine Liste von Anteilen (das wird die \(x\)-Achse), und eine Liste der kumulierten Merkmalssummen, die diesen Anteilen gehören (das wird die \(y\)-Achse).
Idee der Lorenzkurve
Die Lorenzkurve ist ein beliebtes grafisches Mittel, um so eine Ungleichmäßigkeit zu visualisieren. An ihr kann man ablesen, wie sehr eine Verteilung von einer völlig gerechten Gleichverteilung abweicht.
Erstellen einer Lorenzkurve
Nehmen wir zur Vereinfachung ein Land mit 5 Einwohnern an. Die fünf Personen verdienen 3€, 4€, 5€, 5€ bzw. 18€. Zugegeben, das ist ein sehr kleines Land mit sehr niedrigem Lohn—aber wir möchten es ja einfach halten. Wir möchten nun für diese Einwohner und ihre Einkommensverteilung eine Lorenzkurve bilden.
Zuerst müssen dazu die Merkmalsausprägungen der Einheiten nach der Größe sortiert werden. Das weitere Vorgehen wird anhand der folgenden Tabelle Zeile für Zeile gezeigt.
| Einheit \(i\) | Einheit 1 | Einheit 2 | Einheit 3 | Einheit 4 | Einheit 5 |
|---|---|---|---|---|---|
| Einkommen | 3 | 4 | 5 | 5 | 18 |
| Aufsummiertes Einkommen | 3 | 7 | 12 | 17 | 35 |
| Anteil an der Gesamtsumme (\(y\)-Achse) | 0.086 | 0.2 | 0.343 | 0.486 | 1 |
| Prozent der Ärmsten (\(x\)-Achse) | 20% | 40% | 60% | 80% | 100% |
Zeile für Zeile werden hier die benötigten Punkte für die Lorenzkurve erstellt. In der Konzentrationsmessung dreht sich alles um die sogenannte Merkmalssumme, die in unserem Beispiel das gesamte aufsummierte Einkommen, also 35€ ist (die lila Zelle). In der ersten Zeile steht das tatsächliche Einkommen der jeweiligen Person.
In der zweiten Zeile wird nun Stück für Stück das Einkommen aufsummiert. Für Einheit 3 steht hier z.B. die bisherige Teilsumme von 3€ + 4€ + 5€, also 12€. In der letzten Zelle dieser Zeile sieht man die gesamte Merkmalssumme. Es werden also die kumulierten Häufigkeiten gebildet. Die dritte Zeile ist nichts anderes als die zweite Zeile, geteilt durch die gesamte Merkmalssumme. Hier sieht man also, welcher Anteil des gesamten Einkommens jeweils auf einen Anteil der Bevölkerung abfällt. Diese Zeile wird die \(y\)-Achse in der Lorenzkurve. Die \(x\)-Achse ist in der letzten Zeile abgebildet; sie ist der jeweilige Anteil der Bevölkerung \(\frac{i}{n}\), also bei fünf Einheiten 20%, 40%, 60%, 80% und 100%.
Um die Lorenzkurve zu zeichnen, werden nun einfach diese Punkte in einen Graphen gezeichnet. In der folgenden Abbildung sind die schwarzen Punkte genau die, die aus der oberen Tabelle hervorgehen.
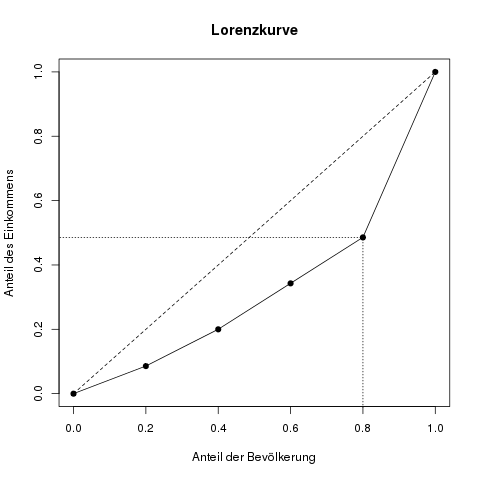
Eine mögliche Lorenzkurve für Einkommensdaten. Die gestrichelte Linie ist die „Gerade der perfekten Gleichverteilung“. Hätte jedes Merkmal den gleichen Anteil, würde die Lorenzkurve nämlich genau auf dieser Geraden liegen. Man liest die tatsächliche Kurve am Beispiel der gepunkteten Linie folgendermaßen ab: „Die ärmsten 80% der Bevölkerung haben 48.6 Prozent des gesamten Einkommens“ (Der genaue Wert stammt aus der Tabelle oben). Umgekehrt kann man dann natürlich über die reichsten 20% der Bevölkerung sagen, dass sie 51.4 Prozent des Einkommens haben.
Eine perfekte Gleichverteilung, wenn also jede Person das gleiche Einkommen hätte, wird in der Lorenzkurve durch eine Gerade vom Punkt (0,0) zu (1,1) dargestellt. In der obigen Abbildung ist diese Gerade durch eine gestrichelte Linie eingezeichnet. Hier könnte man ablesen, dass die ärmsten 20% genau 20% des Einkommens hätten, usw.—wobei es bei einer absolut fairen Gleichverteilung ja eigentlich keine „ärmsten“ 20% gibt. Die entsprechende (nicht sehr spannende) Lorenzkurve ist in Kurve (d) unten dargestellt.
Das andere Extrem wäre eine Verteilung, bei der eine einzelne Person das komplette Einkommen hätte, und alle anderen gar nichts. Diese Lorenzkurve sieht man in der Kurve (c) unten.
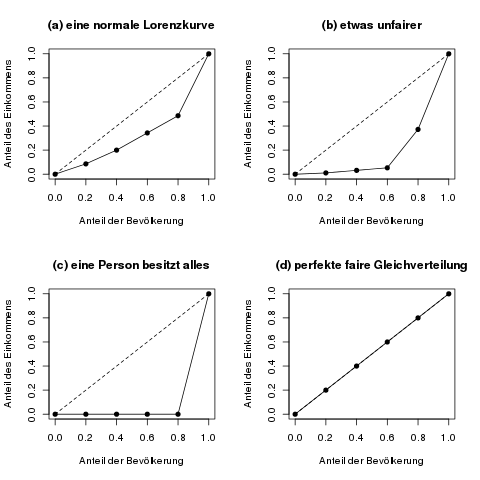
Vier beispielhafte Lorenzkurven. Kurve (a) ist eine übliche Kurve, die wir oben schon gesehen haben. Kurve (b) ist etwas unfairer, hier sind 60% (also drei von fünf) der Einwohner noch sehr arm. Kurve (c) ist für fünf Personen das unfairste Extrem, da 80% der Personen (vier von fünf) gar nichts besitzen. Kurve (d) ist die fairste Lorenzkurve, nämlich eine Gerade vom Punkt (0,0) zum Punkt (1,1).
Mathematische Definition der Lorenzkurve
Wenn man seine Studenten ärgern möchte, definiert man die Lorenzkurve so:
Für gegebene Daten \(x_j, j=1,\ldots,n\) bestimmt man die Punkte \((u_j, v_j)\) der Lorenzkurve durch
\[ \begin{align*} u_j & = \frac{j}{n} \\ v_j & = \frac{\sum_{i=1}^j x_{(i)}}{\sum_{i=1}^n x_{(i)}} \end{align*} \]
Das ist eine zunächst unverständliche, aber kurze Zusammenfassung der Tabelle im vorherigen Beispiel. Die Punkte \(u_j\) sind die summierten Anteile, also die \(x\)-Achse, und die Punkte \(v_j\) die Anteile der Merkmalssumme (im Zähler steht die bisherige Summe bis zum \(j\)-ten Punkt, und im Nenner die gesamte Merkmalssumme)—also die \(y\)-Achse.
Es gibt übrigens noch eine stetige Variante der Lorenzkurve. Die ist allerdings relativ kompliziert über Integrale zu berechnen, und wird daher in Einführungsveranstaltungen zur Statistik meist nicht behandelt.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!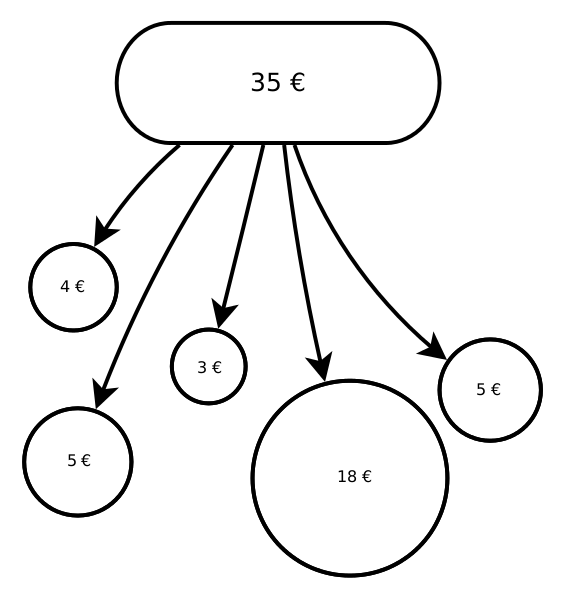
Hallo Alex,
ich danke Ihnen dafür dass Sie diesen Crashkurs kostenlos anbieten.
Dank Ihnen habe ich in kurzer Zeit mehr gelernt als in den 6 Monaten in der Vorlesung.
Echt klasse beschrieben und Top Beispiele auf Universität Niveau.
Mit freundlichen Grüßen
Bald Tutor in Statistik
Das ist wirklich klasse beschrieben, nun verstehe ich das deutlich besser als in der Vorlesung. Tolle Arbeit, weiter so 🙂
Hallo Alex,
Meine Frage ist: die Lorenzkurve ist also immer eine Momentaufnahme von Einkommen. Aber angenommen ich habe vor 20 Jahren das gleiche verdient wie mein Kollege.Ich habe aber gesparrt und habe nun nach 20 Jahren immer noch das gleiche Einkommen wie mein Kollege aber noch ein zusätzliches Einkommen vom gesparten was er nicht hat. Dieses Zusatzeinkommen spiegelt sich normal bei der Berechnung des Momentaneinkommen wieder? Maw ist die Lorenzkurve immer nur ein Istwert oder auch eine historische Aussage über Einkommen die sich durch besseres wirtschaften summiert haben?
Hallo Johann,
es geht immer nur um eine Ist-Aufnahme. Wenn du heute 20.000 Einkommen und 500 Zinsen bekommst, sind es eben 20.500 insgesamt. Für Vergleiche über die Zeit würde sich eine Lorenzkurve nicht eignen.
VG,
Alex
Lieben Dank für eine einfache und schlüssige Erklärung! Sie sollen bitte die Lehrbücher schreiben, Studenten wären Ihnen sehr dankbar dafür!
Vielen Dank! Ich bin tatsächlich gerade dabei, ein Lehrbuch zu schreiben 🙂
Hallo Alex,
gibt es Dein Buch mittlerweile schon zu kaufen?
Du hast das wirklich super gut erklärt!
Vielen Dank dafür 🙂
Hi 🙂
Die Ebooks gibt es schon eine Weile, aber die Erklärungen sind noch nicht vollständig – ich werde sie zuerst fertig schreiben, und dann in ein PDF verpacken.
VG
Alex
Hallo Alex,
möchte sowas ebenfalls darstellen jedoch in RStudio..
funktioniert sowas auch wenn ich das Einkommen z.B. in: unter 1000 Euro, 1000 bis unter 1500 Euro, etc. aufteile? und nicht ein festes Einkommen angebe wie 1000 / 2000 / 3000 Euro?
Viele Grüße!!
Wow, endlich kapiert, wie man die x-Werte berechnet! Danke ihr habt mir echt geholfen.
LG Tim
Achso und ich hätte noch eine persönliche Frage. Hat jemand noch so eine schlüssige Erläuterung zum Variationskoeffizienten?
Das würde mir sehr helfen.
Lg Marie
Hallo,
Ich hab da mal eine Frage. Könnte es sein das in diesem Teil ein Fehler unterlaufen ist?
„Umgekehrt kann man dann natürlich über die reichsten 20% der Bevölkerung sagen, dass sie 51.4 Prozent des Einkommens haben.“
Müssten es nicht 8,6% laut Tabelle sein?
Lg Marie
Nein, die ärmsten 20% haben 8.6%. Die reichsten 20% haben 51.4%, weil die ärmsten 80% die restlichen 48.6% haben (und 51.4% + 48.6% sind dann 100%).
Ist das so verständlich? Ist ein bisschen eklig und leicht zu verwechseln mit den ärmsten/reichsten etc., ich weiss 🙂
Hallo,
ist es dann richtig, dass im weiteren Verlauf, wenn man es aus der Richtung der Reichsten betrachtet,
dass 20% der reichsten 51,4 %,
und 40% der reichsten 65,7% ,
und 60% der reichsten 80%
und 80% der reichsten 91,4% Anteil am Gesamteinkommen haben?
LG Esra
Hallo Esra,
genau, wenn die ärmsten 60% insgesamt 48.6% haben, dann haben die restlichen Leute, also die 40% reichsten, das restliche Geld, also 51.4%. 🙂
VG,
Alex
wie berechnet man die Werte der x-Achse „Prozent der Ärmsten“?
Hi Elisa,
ich habe den Teil im Artikel ein bisschen ausführlicher erklärt, ich hoffe jetzt ist es klarer.
Bei \(n\) Personen sind die Werte der \(x\)-Achse einfach \(\frac{1}{n}\), \(\frac{2}{n}\), \(\frac{3}{n}\) etc.
Bei uns also \(\frac{1}{5}\), \(\frac{2}{5}\), \(\frac{3}{5}\), \(\frac{4}{5}\) und \(\frac{5}{5}\).
Danke auch dafür!