Man verwendet Venn-Diagramme, um zwei oder mehrere Mengen und deren Beziehungen zueinander darzustellen. Man kann es auch gut dazu verwenden, um Regeln der Wahrscheinlichkeitsrechnung sehr einfach zu visualisieren, weshalb wir sie uns hier anschauen werden.
Ein Venn-Diagramm für zwei Mengen \(A\) und \(B\) sieht wie folgt aus:
Wir halten uns dabei durchgehend an ein beispielhaftes Zufallsexperiment:
Wir werfen einen Würfel, und notieren uns die Augenzahl. Die möglichen Ergebnisse sind also \(\{ 1, 2, 3, 4, 5, 6\}\) (die Menge aller möglichen Ereignisse wird mit \(\Omega\) bezeichnet). Wir definieren außerdem zwei Ereignisse \(A\) und \(B\):
\[ A: \text{Es wurde eine gerade Zahl }\mathrm{gew\ddot{u}rfelt} \]
\[ B: \text{Es wurde eine Zahl von 1 bis 3 }\mathrm{gew\ddot{u}rfelt} \]
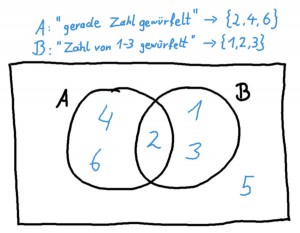
Das Ereignis \(A\) beinhaltet also die Zahlen 2, 4, und 6, und das Ereignis \(B\) umfasst die 1, 2, und 3. Hier fällt auf, dass die 2 in beiden Ereignissen vorkommt. In unserem Venn-Diagram wären die Ereignisse so aufgeteilt:
Man sieht hier ein großes Rechteck, das das ganze „Universum“ \(\Omega\), also alle möglichen Ereignisse darstellt. Innerhalb aller möglichen Eregnisse befinden sich die Mengen \(A\) und \(B\), die jeweils nur einen Teil aller möglichen Ereignisse beschreiben. Im Kreis von \(B\) liegen zum Beispiel die 1, 2, und 3. Die 2 liegt zudem auch im Kreis von \(A\). Die 5 kommt weder in \(A\), noch in \(B\) vor, liegt also im Bereich von \(\Omega\), also außerhalb beider Kreise.
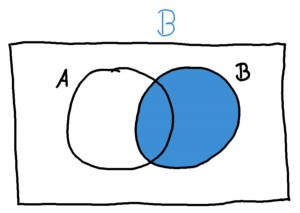
Die Menge \(B\) lässt sich nun durch diesen blauen Kreis darstellen:
Wenn ich dich den Würfel rollen lasse, und sage, bei einem Ergebnis aus \(B\) hast du gewonnen, dann hoffst du also auf eine 1, 2, oder 3 als Ergebnis. Vergleiche dieses Bild nochmal mit dem oberen Bild, in dem die Zahlen eingetragen sind, falls du gerade nicht folgen konntest.
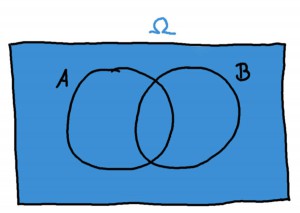
Die Menge \(\Omega\) ist, wie schon gesagt, die Menge aller möglichen Ereignisse:
Angenommen, du spielst nun dasselbe Spiel, aber ich sage dir dass du bei einem Ergebnis aus \(\Omega\) gewonnen hast, welche Zahlen sind also günstig für dich?
Der „nicht“-Operator
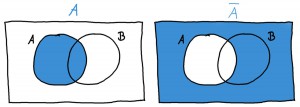
Wenn man am Gegenteil eines Ereignisses interessiert ist, setzt man einen Querbalken darüber. Am Beispiel des Ereignisses \(A\) sieht das so aus:
Links ist das Ereignis \(A\) abgebildet (welche Zahlen auf dem Würfel beinhaltet das?), und rechts sein Gegenteil, nämlich \(\bar{A}\). Überlege dir auch, welche Zahlen das Ereignis \(\bar{A}\) beinhaltet.
Der „oder“-Operator (Vereinigungsmengen)
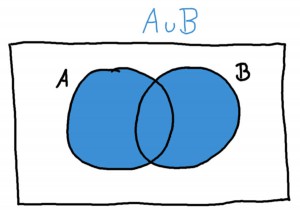
Möchte man die einzelnen Elemente zweier Mengen \(A\) und \(B\) in einen Topf werfen, also vereinigen, verwendet man dazu das Symbol \(\cup\). Die Menge aller Elemente, die in \(A\) oder \(B\) enthalten sind, ist also \(A \cup B\).
Versuche, die Menge \(A \cup B\) in einem Venn-Diagramm zu zeichnen. Überlege dir auch, welche Elemente sie beinhaltet (und welche nicht).
Der „und“-Operator (Schnittmengen)
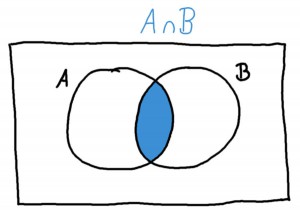
Mit dem „und“-Operator \(\cap\) bezeichnet man die Schnittmenge zweier Mengen \(A\) und \(B\). Man erhält als Ergebnis nur die Elemente, die sowohl in \(A\) als auch in \(B\) enthalten sind:
Für unser Beispiel mit den Würfeln bedeutet das: In \(A \cap B\) sind die Zahlen enthalten, die sowohl gerade als auch kleiner oder gleich 3 sind – also nur die 2: \(A \cap B = \{2\}\).
Kombinationen von Operatoren
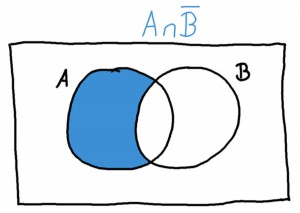
Mit diesen drei Operatoren, der Vereinigungs- und Schnittmenge sowie der Negation (also dem Querbalken), kann man nun zusammen jede mögliche Kombination der beiden Mengen \(A\) und \(B\) erstellen. Zum Beispiel kann man sich alle Elemente ansehen, die zwar in \(A\), aber nicht in \(B\) enthalten sind:
Diese Menge \(A \cap \bar{B}\) enthält die Zahlen 4 und 6, da das die geraden Zahlen aus \(A\) sind, die nicht in der Menge \(B\) vorkommen.
Eine weitere Möglichkeit, diese Menge darzustellen, ist mit dem Differenzoperator \(\setminus\). Es bedeutet also \(A \setminus B\) „A ohne B“, also dasselbe wie \(A \cap \bar{B}\).
Zwei abschließende Aufgaben zum Verständnis
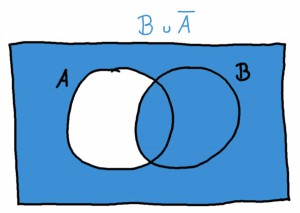
(a) Zeichne die Menge \(B \cup \bar{A}\) in einem Venn-Diagramm und bestimme, um welche Zahlen auf dem Würfel es sich in unserem Beispiel handelt.
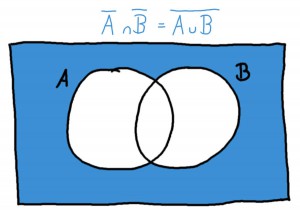
(b) Zeichne die Menge \(\bar{A} \cap \bar{B}\) und bestimme ebenso die resultierende Menge im Beispiel.
Wahrscheinlichkeiten mit Venn-Diagrammen
Man kann nun Laplace-Wahrscheinlichkeiten mit Venn-Diagrammen illustrieren. Möchte ich in dem oben verwendeten Beispiel die Wahrscheinlichkeit für das Ereignis \(B \cup \bar{A}\) bestimmen, können wir durch ein Venn-Diagramm schnell bestimmen, dass das Ereignis \(B \cup \bar{A}\) die Zahlen 1, 2, 3 und 5 auf dem Würfel umfasst. Das sind 4 verschiedene Ergebnisse von 6 möglichen Ergebnissen, also ist
\[ \mathbb{P}(B \cup \bar{A}) = \frac{4}{6} = \frac{2}{3} \]
Beachte aber, dass das einfache Abzählen (also die Idee „4 von 6 möglichen Ergebnissen, das heißt eine Wahrscheinlichkeit von \(\frac{4}{6}\)“) nur bei Laplace-Experimenten funktioniert, d.h. nur bei Experimenten, wo jedes mögliche Ergebnis mit derselben Wahrscheinlichkeit auftritt.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!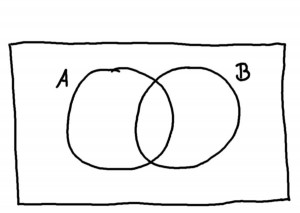
aus dem obigen Text:
Wir werfen einen Würfel, und notieren uns die Augenzahl. Die möglichen Ergebnisse sind also {1,2,3,4,5,6} (die Menge aller möglichen Ereignisse wird mit Ω bezeichnet). Wir definieren außerdem zwei Ereignisse A und B:
Hallo Alex,
ich bin völlig begeistert von deinem Blog über Statistik. Es hilft mir unglaublich die ganze Sache zu verstehen. Vielen Dank dafür!
Ich glaube einen kleinen Fehler gefunden zu haben. Den obigen Testausschnitt habe ich unter dem ersten Venn-Diagramm heraus kopiert. In der Klammer: (die Menge aller möglichen Ereignisse wird mit Omega…
muss das nicht heißen: (die Menge aller möglichen Ergebnisse…
LG Christine
Hallo Christine,
vielen Dank für das Lob 🙂
Ich benutze die Begriffe Ergebnis und Ereignis hier synonym. Ich wollte etwas Abwechslung in den Text bringen 🙂
Viele Grüße
Alex
Hallo,
Sollte es bei Aufgabe nicht eher heißen, dass die Zahl 5 weder in A noch in B enthalten ist?
2 ist ja bei A und bei B enthalten. und Laut der blauen Farbunterlegung käme auch nur die 5 in Betracht
lg
Oh, du hast recht – ich habe es gerade ausgebessert. Vielen Dank! 🙂