Behaltet im Kopf, was die lineare Regression macht. Sie zeichnet eine Gerade durch ein Streudiagramm. Das funktioniert in vielen Fällen gut, aber in anderen Fällen leiten die Ergebnisse zu Fehlschlüssen.
Hier ist ein Beispiel: Es wurde auf einer Teststrecke für 100 Autos deren Geschwindigkeit gemessen, und dann der Bremsweg bei einer Vollbremsung. Wer sich noch an die Fahrschule erinnert, weiß, dass der Bremsweg annähernd so berechnet werden kann:
\[ x = \frac{v}{10} \cdot \frac{v}{10} \cdot \frac{1}{2} \]
Das ist eine quadratische Formel. Sie lässt sich kürzen zu \(x = v^2 / 200\). Misst man jetzt auf der Teststrecke 100 Autos, könnte das Ergebnis so aussehen:

Die Regressionsgerade im rechten Bild ist in dieser Situation keine gute Wahl. Der Grund ist, dass eine der Annahmen des linearen Modells verletzt wurden.
Es gibt verschiedene Möglichkeiten, die Annahmen zu formulieren, und die genaue Anzahl der Annahmen ist dann auch abhängig von der Formulierung. In meiner Darstellungsweise gibt es die folgenden vier wichtigen Annahmen:
1. Linearer Zusammenhang
Die erste Annahme wurde in unserem obigen Beispiel gleich verletzt: Für ein lineares Modell muss der Zusammenhang natürlich auch linear sein. Das erste Bild ist ein Beispiel dafür, das zweite und dritte ein Gegenbeispiel:
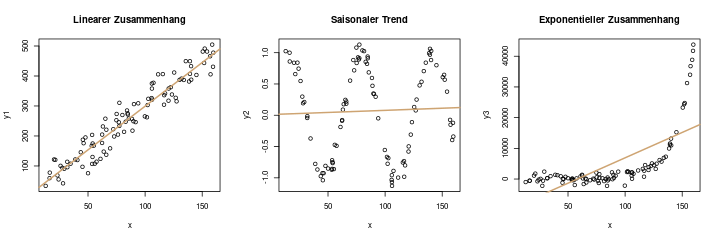
Mathematisch sieht die Annahme für einen linearen Zusammenhang einfach so aus:
\[ \mathbb{E}(y_i) = a + b \cdot x \]
Das ist die Formulierung für das lineare Modell. Ein mögliches Gegenbeispiel, im zweiten Bild, sähe z.B. so aus: \(\mathbb{E}(y_i) = a + \sin(x) / 10\)
2. Normalverteilung der Residuen
Die Residuen sind die Abstände zwischen einer Beobachtung und deren Vorhersage auf der Regressionsgeraden. (In diesem Artikel werden Residuen nochmal genauer erklärt.) Möchte man nun nicht nur eine „gute“ Gerade durch die Daten ziehen, sondern auch Eigenschaften dieser Geraden testen, dann müssen als Voraussetzung dafür die Fehlerterme einer Normalverteilung folgen. Das hat den Grund, dass dann ein einfacher Hypothesentest für die Parameter (also z.B. Steigung der Geraden = 0) durchgeführt werden kann.
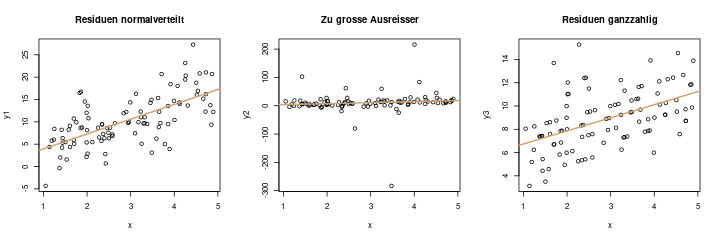
Das linke Bild zeigt eine Regressionsgerade, um die die Fehlerterme mit einer „schönen“ Normalverteilung streuen. Das ist die Idealsituation.
Das zweite Bild, in der Mitte, sieht anders aus. Hier gibt es sehr große Ausreißer, die die Schätzung stark beeinflussen würden, und zu ungenauen Konfidenzintervallen und Testaussagen führen würden. (Wer es genau wissen möchte: Ich habe die Residuen in diesem Diagramm als \(t\)-Verteilung mit einem Freiheitsgrad simuliert)
Das dritte Bild ist ein weiteres Beispiel für eine „falsche“ Verteilung: Hier sind die Residuen in etwa in ganzzahligen Abständen zur Regressionsgerade. Das ist ein sehr realitätsfernes Beispiel, es wird wohl nie vorkommen, aber es veranschaulicht sehr schön, welche Situationen durch die Modellannahme der normalverteilten Residuen „nicht erlaubt“ sind.
In eine Formel verpackt sieht diese Annahme nun so aus:
\[ \begin{align*} y_i &= a + b\cdot x_i + \epsilon_i \\ \epsilon_i &\sim \mathcal{N}(0, \sigma^2) \end{align*} \]
Die zweite Zeile verlangt, dass die Residuen \(\epsilon\) normalverteilt sind. In dieser Formel steckt eigentlich auch schon die nächste Annahme mit drin:
3. Gleichbleibende Varianz der Residuen
Diese Annahme besagt, dass die Varianz der Residuen sich über die \(x\)-Achse nicht verändern soll. Das linke Bild zeigt wieder ein positives Beispiel, und das rechte Bild zeigt, wie es nicht aussehen soll:
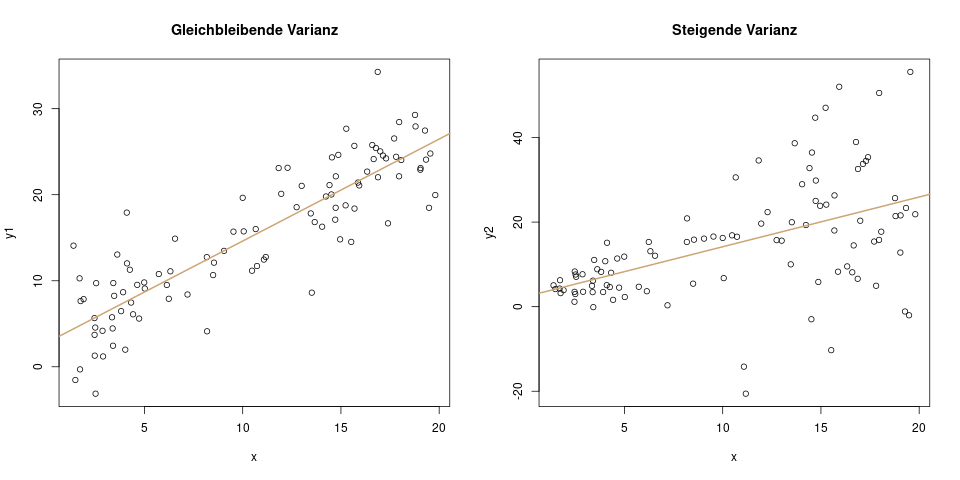
Die gleichbleibende Varianz (man sagt auch Homoskedastizität dazu – mein absolutes Lieblingswort) steckt auch schon in der oberen Formel drin. Man verlangt nämlich, dass für jede Beobachtung \(i\) die Varianz gleich ist. Es ist also \(\epsilon_i \sim \mathcal{N}(0, \sigma^2)\), und nicht \(\epsilon_i \sim \mathcal{N}(0, \sigma_i^2)\). Der Unterschied ist sehr klein: Statt \(\sigma^2\) steht in der zweiten Formel \(\sigma_i^2\). Das tiefgestellte \(i\) bedeutet, dass die Varianz hier für jede Beobachtung \(i\) unterschiedlich ist. Im rechten Bild wäre also z.B. für die erste Beobachtung \(\sigma_1^2 = 0.6\), und für die letzte Beobachtung \(\sigma_{100}^2 = 12.4\). Das bedeutet: unterschiedliche Varianzen, und genau das ist im linearen Modell nicht erlaubt. Die Streuung muss für jede Beobachtung gleich groß sein.
4. Unabhängigkeit der Residuen
Mit Unabhängigkeit ist das Folgende gemeint: Wenn ich den Fehlerterm für eine bestimmte Beobachtung kenne, dann darf mir das keine Information über den Fehlerterm für die nächste Beobachtung liefern. Das ist zum Beispiel im folgenden Bild der Fall:
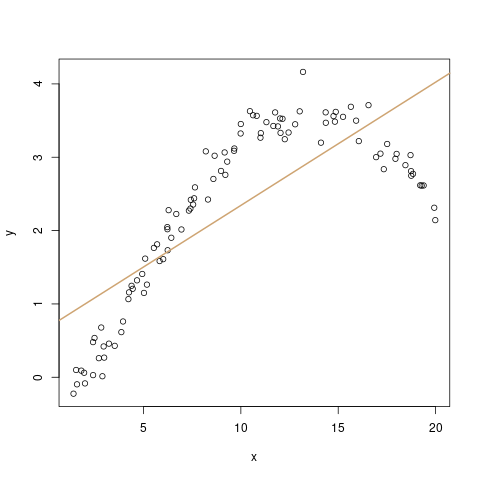
Hier ist natürlich gleichzeitig die Annahme des linearen Einflusses verletzt (Verletzungen von Modellannahmen kommen selten alleine). Aber zusätzlich sind die Residuen abhängig voneinander: am linken Ende der \(x\)-Achse sind alle Residuen negativ, d.h. alle Punkte liegen unter der Regressionsgeraden. Die Abhängigkeit in diesem Bild heißt dann etwa: Wenn ich weiß, dass für Beobachtung \(i=10\) ein positives Residuum gibt, dann kann ich dadurch Schlüsse über das Residuum für die nächste Beobachtung \(i=11\) ziehen – es ist nämlich wahrscheinlich auch positiv.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hey, ich habe eine Frage. Zur Berechnung einer Regression habe ich mit meinen Daten vorab alle notwendigen Voraussetzungen überprüft und festgestellt, dass nahezu keine davon zutrifft. In meiner Hypothese habe ich aber einen gerichteten Zusammenhang aufgestellt. Gibt es ein anderes Verfahren, mit dem ich diesen gerichteten Zusammenhang feststellen/nicht feststellen kann?
Meines Wissens nach ist entweder das Verfahren gegen Abweichungen robust (sehe ich hier nicht, weil ja quasi keine der Voraussetzungen erfüllt wird) oder es gibt ein Ausweichverfahren. Nur welches? Ich stehe auf dem Schlauch.
Danke vorab für einen Tipp – falls Du ihn hast 🙂
Ja, es gibt unzählig viele Ausweichverfahren. Welches davon passt, kommt darauf an welche Voraussetzungen bei einer linearen Regression nicht erfüllt wären.
Ein paar Stichworte für mögliche Lösungen sind die robuste Regression, Quantilregression, generalisierte lineare Modelle, oder generalisierte additive Modelle. Die richtige Wahl für deine Situation ist aber wahrscheinlich zu komplex um das hier zu erledigen 🙂