Ein Residuum, ganz grob gesagt, ist für eine bestimmte Beobachtung \(i\) der Fehler, den die Vorhersage des gerechneten Regressionsmodells für diese Beobachtung gemacht hat. Sie sind eine wichtige Kennzahl bei der Regression. Man schaut sie sich typischerweise während der Modelldiagnose genauer an, um zu überprüfen ob die Annahmen dieses Modells plausibel sind.
Im gegebenen Datensatz hat jede Beobachtung \(i\) einen wahren, beobachteten Wert für die Zielgröße \(y_i\). Nachdem nun auf diesen Daten ein Regressionsmodell angepasst wurde, hat jede Beobachtung \(i\) zusätzlich einen vorhergesagten Wert für die Zielgröße, den wir \(\hat{y}_i\) nennen.
Das Residuum wird nun meistens mit \(\hat{\epsilon}_i\) bezeichnet. Es bezeichnet den Fehler, den das Regressionsmodell mit der Vorhersage für diese Beobachtung \(i\) gemacht hat.
Man berechnet das Residuum für die \(i\)-te Beobachtung durch
\[ \hat{\epsilon}_i = y_i – \hat{y}_i \]
Grafisch kann man sich das schön veranschaulichen. Das Residuum für eine Beobachtung ist der farbig markierte Abstand:
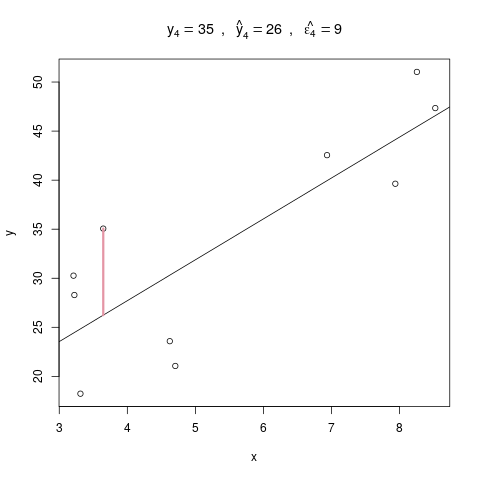 Für die vierte Beobachtung in dieser Grafik liegt der wahre \(y\)-Wert bei 35, und der vorhergesagte (also der auf der Regressionsgeraden) bei 26. Das Residuum, der Fehler der Schätzung, liegt also bei \(\hat{\epsilon}_4 = 35 – 26 = 9\).
Für die vierte Beobachtung in dieser Grafik liegt der wahre \(y\)-Wert bei 35, und der vorhergesagte (also der auf der Regressionsgeraden) bei 26. Das Residuum, der Fehler der Schätzung, liegt also bei \(\hat{\epsilon}_4 = 35 – 26 = 9\).
Falls der wahre Wert unter der Regressionsgeraden liegt, wird das Residuum natürlich negativ.
Die Residuen berechnet man nach dem Rechnen eines Regressionsmodells für jede Beobachtung. Wie oben bereits gesagt, werden diese Kennzahlen für die Modelldiagnose verwendet. Die meisten Annahmen des Modells, so wie die Annahme der Normalverteilung, müssen nämlich nur für die Residuen gelten, nicht z.B. für die Zielgröße \(y\).

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Pingback: So gelingt eine Mixed Model Analyse in SPSS | NOVUSTAT