Die Korrelation ist eine Möglichkeit, den Zusammenhang zwischen zwei Variablen zu beschreiben. Der Pearson-Korrelationskoeffizient \(r\) ist einer von vielen Möglichkeiten dazu, und meiner Meinung nach die einfachste, am ehesten intuitive.
Mit der Korrelation mißt man den linearen (dazu später mehr) Zusammenhang zwischen zwei Variablen. Der Wert kann zwischen -1 und 1 liegen, und wird wie folgt interpretiert:
- \(r \approx 0\): Wenn zwei Variablen eine Korrelation von ungefähr Null haben, lässt sich kein Zusammenhang erkennen. Die Variablen sind unkorreliert. Eine Korrelation von 0 erwartet man z.B. zwischen der Hausnummer und der Körpergrösse einer Person.
- \(r > 0\): Wenn \(r\) größer als Null ist, spricht man von einer positiven Korrelation. Größere Werte von \(X\) gehen dann einher mit größeren Werten von \(Y\). Das ist zum Beispiel bei der Körpergrösse und der Schuhgrösse einer Person der Fall: Grössere Menschen haben meistens auch grössere Schuhe.
- \(r < 0\): Wenn \(r\) negativ ist, dann hängen höhere Werte von \(X\) mit niedrigeren Werten für \(Y\) (und umgekehrt) zusammen. Betrachtet man etwa die Anzahl der Skiurlauber und die Aussentemperatur, sieht man, dass bei niedrigeren Temperaturen mehr Urlauber kommen.
Sehen wir uns ein paar grafische Beispiele an:
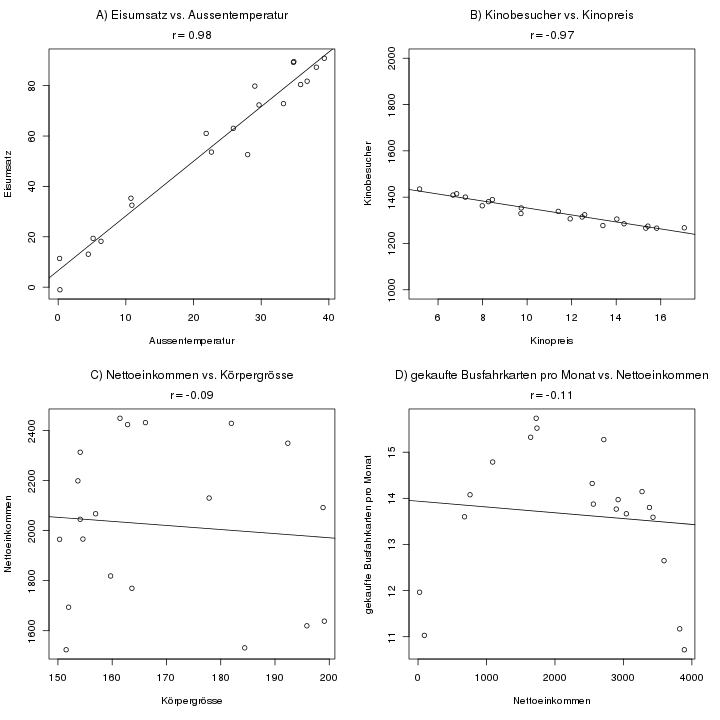
Hier sieht man vier Beispiele für Datensätze mit zwei Variablen. Gezeigt sind die X- und Y-Werte, sowie der jeweilige Korrelationskoeffizient \(r\), und eine Regressionslinie.
- A)
- Hier sieht man eine starke positive Korrelation. Die hohe Korrelation deutet darauf hin, dass ein Zusammenhang zwischen Außentemperatur und Umsatz einer Eisdiele besteht.
- B)
- Ein Beispiel für eine negative Korrelation. Höhere Preise für Kinokarten gehen mit weniger Besuchern einher. Hier fällt auch auf, dass die Steigung der Geraden keine Rolle spielt. Der Korrelationskoeffizient bemerkt nur, wie „perfekt“ der lineare Zusammenhang ist, aber nicht, wie stark er ist.
- C)
- Sieht man sich Daten für Körpergrösse und Nettoeinkommen an, erkennt man keinen Zusammenhang. Hier ist sogar eine leicht negative Korrelation zu erkennen, die man aber wohl als zufällig betrachten kann.
- D)
- Ein Beispiel für die Grenzen der Korrelation: Sehr arme Menschen können sich keine Busfahrkarten leisten, und sehr reiche Menschen fahren eher Auto. Der Zusammenhang ist hier nicht linear, sondern folgt eher einer Parabel. Man sieht eine Abhängigkeit zwischen dem Einkommen und der gekauften Busfahrkarten, aber die lineare Korrelation erkennt ihn nicht.
Um den Korrelationskoeffizienten \(r\) für zwei Variablen zu berechnen, gibt es zwei Formeln, wo bei beiden natürlich das Gleiche rauskommt. Manchmal ist allerdings die eine oder andere Formel einfacher in den Taschenrechner einzutippen.
Für die Formeln sollte man mit dem Summenzeichen umgehen können, das im entsprechenden Artikel erklärt wird.
Formel 1: \[ r = \frac{\sum_{i=1}^n (x_i – \bar{x}) (y_i – \bar{y})}{ \sqrt{\sum_{i=1}^n (x_i – \bar{x})^2} \cdot \sqrt{\sum_{i=1}^n (y_i – \bar{y})^2} } \]
Formel 2: \[ r= \frac{\sum_{i=1}^n x_i y_i – n \bar{x} \bar{y}}{\sqrt{\sum_{i=1}^n x_i^2 – n\bar{x}^2} \cdot \sqrt{\sum_{i=1}^n y_i^2 – n\bar{y}^2} } \]
Die zweite Formel ist einfacher und schneller im Taschenrechner zu berechnen. Wenn allerdings sehr große Zahlen für \(x\) oder \(y\) vorkommen, werden die Summen der Quadrate (die Terme \(\sum_{i=1}^n x_i^2\)) zu gross, und der Speicher des Taschenrechners spielt nicht mehr mit.
Beispielaufgabe
Schauen wir uns die Berechnung von \(r\) mit beiden Formeln anhand eines Beispiels an:
| Person \(i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| \(x_i\): Zigaretten pro Tag | 4 | 21 | 2 | 11 | 14 | 2 | 6 |
| \(y_i\): Todesalter | 70 | 63 | 82 | 65 | 61 | 74 | 84 |
Überlege dir vorher, ob du eine positive oder negative Korrelation erwartest. Du kannst auch ein Streudiagramm der Daten zeichnen, um im Vorfeld etwas mehr Klarheit zu bekommen.
Für beide Formeln müssen wir zuerst die Mittelwerte \(\bar{x}\) und \(\bar{y}\) berechnen:
\[ \bar{x} = \frac{1}{7} \cdot (4+21+2+11+14+2+6) = 8.57\]
\[ \bar{y} = \frac{1}{7} \cdot (70+63+82+65+61+74+84) = 71.29\]
Formel 1
Am einfachsten ist es, die Formel in drei Schritten zu berechnen, und die Zwischenergebnisse aufzuschreiben, und am Ende den gesamten Bruch auszurechen. Beginnen wir mit dem Zähler:
\[ \begin{align*} \sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y}) = & (4-8.57)\cdot (70-71.29)+\\ & (21-8.57)\cdot (63-71.29)+\\ & (2-8.57)\cdot (82-71.29)+\\ & (11-8.57)\cdot (65-71.29)+\\ & (14-8.57)\cdot (61-71.29)+\\ & (2-8.57)\cdot (74-71.29)+\\ & (6-8.57)\cdot (84-71.29) \\ & = -289.14 \end{align*} \]
Nun die beiden Teile im Nenner:
\(\sqrt{\sum_{i=1}^n (x_i – \bar{x})^2} = \sqrt{(4-8.57)^2 + (21-8.57)^2 + \ldots +(6-8.57)^2} = 17.43\)
\(\sqrt{\sum_{i=1}^n (y_i – \bar{y})^2} = \sqrt{(70-71.29)^2 + \ldots +(84-71.29)^2 } = 22.35\)
Zusammen in die Formel von oben eingesetzt ergibt sich die Korrelation:
\[ r= \frac{-289.14}{17.43 \cdot 22.35} = -0.74 \]
Formel 2
Mit diesem Weg hat man mehr Zwischenergebnisse als mit Formel 1, und kann sich im Taschenrechner nicht so leicht vertippen. Man berechnet nacheinander die folgenden fünf Werte:
- \(\bar{x} = 8.57\)
- \(\bar{y} = 71.29\)
- \(\sum_{i=1}^n x_iy_i = 4\cdot 70 + 21\cdot 63 + 2\cdot 82 + 11\cdot 65 + 14\cdot 61 + 2\cdot 74 + 6\cdot 84 = 3988\)
- \(\sum_{i=1}^n x_i^2 = 4^2+21^2+2^2+11^2+14^2+2^2+6^2 =818\)
- \(\sum_{i=1}^n y_i^2 = 36071\)
Diese Werte setzt man nun in die Formel ein:
\[ r = \frac{3988 – 7\cdot 8.57 \cdot 71.29}{\sqrt{818 – 7\cdot 8.57^2} \cdot \sqrt{36071 – 7\cdot 71.29^2}} = -0.74 \]
Wie man sieht, ist die zweite Variante angenehmer zu rechnen, könnte aber problematisch werden, wenn z.B. Zahlen über 10,000 quadriert und summiert werden.
Herleitung über die empirische Kovarianz
Dieser Abschnitt wird ein bisschen mathematisch, kann also gerne übersprungen werden, wenn man nicht an der Intuition hinter der Formel interessiert ist.
Die Korrelation ist eigentlich eine standardisierte Version der Kovarianz zweier Variablen. Die Kovarianz ist definiert als
\[ \text{Cov}(x, y) = \frac{1}{n-1} \sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})\]
Der Betrag der Kovarianz bewegt sich zwischen \(0\) (bei unkorrelierten Variablen) und \(s_x \cdot s_y\) (bei perfekt korrelierten Variablen). Dabei ist \(s_x\) die Standardabweichung von \(X\), und \(s_y\) die von \(Y\). Das Vorzeichen der Kovarianz lässt nun schon erkennen, in welche Richtung der Zusammenhang zweier Variablen geht, genauso wie bei der Korrelation. Aber ihr Wert ist abhängig von der Varianz von \(x\) und \(y\). Daher wird die Kovarianz standardisiert, indem man durch die Standardabweichungen von \(x\) und \(y\) teilt – dadurch erhält man die Korrelation, deren Wertebereich nun von -1 bis 1 geht:
\[ r = \frac{\text{Cov}(x, y)}{s_x \cdot s_y} \]
Die Faktoren \(\frac{1}{n-1}\) stehen im Zähler und im Nenner, und kürzen sich heraus, wodurch die Formel 1 oben entsteht.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hey Alex,
danke für deine Erklärungen!
Eine Frage hätte ich noch: sicher dass man 1/(n-1) rauskürzen kann?
Denn im Nenner (sprich bei der Berechnung der Standardabweichung) steht 1/(n-1) unter Wurzel.
Besten Dank und LG
Freddy
Hi! Das kann man kürzen, ja. Im Zähler steht einmal 1/n-1, und im Nenner steht zweimal 1/n-1, allerdings unter der Wurzel (multipliziert ist das dann wieder 1/n-1). Die beiden Faktoren kann man kürzen.
Pingback: Kausalität, Korrelation, Scheinkorrelation und der Korrelationskoeffizient - du-bist-grossartig.de
Lieber Alex,
Ich wollte mich nur herzlich bei dir für diese tolle und sehr verständlich erklärte Berechnung des Korrelationseffizienten bedanken! Habe überall im Web, auch auf youtube nach einer simplen Darstellung gesucht – deine war die Einzige die mir bei der Lösungsfindung geholfen hat.
Weiter so und DANKE nochmal!
LG
San
Ich habe eine Frage zur positiven und negativen Korrelation. Im Beispiel A (positiv) nehmen beide Werte zu (Temperatur und Eis Umsatz) im Beispiel B (negativ) nimmt ein Wert zu und einer ab (Kinopreis, Besucheranzahl).
Was für eine Korrelation hat man wenn beide werte abnehmen z.B die Anzahl der Sportler die draußen Sport treiben und die Außentemperatur? Positiv oder negativ?
Eine positive, denn: Die folgenden beiden Aussagen bedeuten genau dasselbe:
„Wenn die Temperatur fällt, gibt es weniger Sportler“
und
„Wenn die Temperatur steigt, gibt es mehr Sportler“
Du kannst also die erste Aussage umformulieren in die zweite, und hast eine positive Korrelation.
Ein ganz kurzer Einschub. Die Umformulierung ändert nichts daran, ob es eine postive oder eine negative Korrelation ist. Die Umformulierung ist zwar korrekt, aber die Bezeichnung, dass man dann eine positive Korrelation hat (und vorher eine negative) ist falsch! Beide Formulierungen beschreiben eine positive Korrelation.
Eine positive Korrelation bedeutet, dass die beiden so zusammenhängen, dass sie „gemeinsam fallen“ oder „gemeinsam steigen“. Also wird das eine größer, wird es das andere auch. Wird das andere kleiner, wird es das andere auch. Egal welche Formulierung ich wähle.
Eine negative Korrelation bedeutet das Gegenteil: wird das eine größer, sinkt das andere. Und wird das eine kleiner, dann wird das andere größer. Z.B. Mit steigendem IQ sinkt die Dauer der Bearbeitungszeit für Aufgabe X. Anders formuliert ist es immer noch eine negative Korrelation: Mit sinkendem IQ steigt die Dauer der Bearbeitungszeit für Aufgabe X. Auch die Formulierung „mit steigender Bearbeitungszeit sinkt der IQ“ ist korrekt. Aber zeigt noch immer eine negative Korrelation.
Hi Tam,
deine Anmerkung stimmt – allerdings habe ich nicht gesagt dass vorher eine negative Korrelation bestand. Ich glaube da habe ich mich ungünstig ausgedrückt 🙂
Beide Situationen beschreiben natürlich eine positive, nur wird es in der zweiten Art der Formulierung klarer, warum das so ist! 🙂
Viele Grüße
Alex
Hi Alex,
vielen Dank für den Artikel.
Mit welchem Wert beschreibe ich denn dann die Steigung der Geraden?
In Graph B fällt die Besucherzahl um etwa 8% (ganz grob), wenn der Preis um 100% ansteigt.
Welcher Koeffizient beschreibt dieses Verhältnis? Der Korrelationskoeffizient ja eben nicht….
Vielen Dank!
Hi Andreas,
die Steigung kriegt man mit dem Korrelationskoeffizienten nicht raus. Die berechnet man mit einer anderen Methode: der linearen Regression.
Dazu habe ich hier auch einige Artikel. Die Steigung, die du suchst, ist der Parameter \(b\), von dem dort dann gesprochen wird.
Ich hoffe die helfen dir weiter!
VG
Alex
Pingback: Was haben Berufsbildner und Kerzen gemein? | STRIM Unternehmensgruppe
Hi Alex,
kannst du bitte noch was zur Interpretation der Höhe einer Korrelation sagen? Ab wann würde man einen Korrelationskoeffizienten als hoch bzw. niedrig bewerten? Und wäre diese Bewertung gleich für Pearson und Spearman? Danke!
LG
Aleks
Hallo Alex,
das ist wirklich ein sehr erhellender Beitrag. Vielen Dank dafür 🙂
Ich habe hier ein Beispiel, das mich verwirrt, denn es ist immer die Rede vom _linearen_ Zusammenhang zwischen den Daten. Ich habe hier einen eindeutig exponentiellen Zusammenhang zwischen den Daten:
x | f(x)
——–
2 | 231
3 | 330
4 | 528
5 | 825
6 | 1254
7 | 1914
Der Voyage 200 liefert mir bei einer Regression dazu folgende Funktion:
f(x) = 95,06128 x 1,536114^x
Die Punktepaare und die Funktion entsprechen sich sehr gut und der Rechner liefert mir
r = 0,9995398
Das ist aber doch jetzt ein Maß für den _exponentiellen_ Zusammenhang, oder? Wird der Korrelationskoeffizient hier einfach in seiner Bedeutung erweitert?
Ich danke dir für deine Mühe und habe sonst keine weiteren Probleme 🙂
LG throg
Hi,
das ist auf jeden Fall nicht die lineare Korrelation. Es könnte das \(R^2\) aus dem exponentiellen Modell sein… vielleicht sagt da die Anleitung oder ein Forumsbeitrag irgendwo mehr dazu?
Das \(r\) ist ja keine geschützte Marke.. 😀 manche andere Hersteller / Dozenten etc. verwenden das manchmal für andere Dinge, das kann durchaus passieren.
Ah ok, also eher eine ungeschickte Wortwahl, und r bedeutet hier etwas anderes als den von dir beschriebenen Koeffizienten. Danke nochmals…
Hallo,
vielen Dank für die tolle Erklärung! Nur habe ich eine Frage, ich habe von meinem Chef gesagt bekommen, dass bei dem R=… immer auch ein P-Wert dabei sein muss, sonst hat das alles keine Relevanz. Was genau meint er damit?
LG
Monika
Da geht es um einen Korrelationstest. Es wird also die Hypothese getestet, ob der Korrelationskoeffizient 0, oder verschieden von 0 ist.
Hallo
ich habe eine Frage bezüglich der Korrelationen. Ich habe in der Gesamtstichprobe ein N von 60 mache aber daraus 3 Untergruppen. Die Variablen sind bei einem N von 60 normalverteilt in den einzelnen Untergruppen aber nicht mehr. Darf ich trotzdem die Korrelation nach Pearson durchführen? oder muss ich eine Korrelation nach Spearman durchführen weil die Voraussetzung der Normalverteilung nicht mehr erfüllt ist?
Vielen Dank für die Hilfe
Liebe Grüsse
Die Normalverteilung ist nur wichtig, wenn du einen Hypothesentest für die Korrelation durchführen willst. Falls du das nicht brauchst, kannst du trotzdem die Pearson-Korrelation nehmen. Ansonsten solltest du aber auf Spearman ausweichen, ja.
VG
Alex
Hallo Alex,
vielen Dank für die Rechnung, auch ich sitze gerade an meiner Masterarbeit.
Iich möchte gerade die Korrelation zweier Variablen ausrechnen, habe aber das Problem, dass die Stichprobengrößen unterschiedlich groß sind (einmal n = 237 & einmal n = 207).
Darf ich trotzdem einfach die Korrelation berechnen? SPSS wirft mir nen Korrelationskoeffizienten r = .89 heraus, der eigentlich Sinn machen würde.
Rein logisch gesehen dividiert man ja durch n-1, sodass es sich relativieren würde, auch wenn man 2 ns hat. Aber ich würde gerne sicher gehen, ob ich da richtig denke.
Liebe Grüße!
Liebe Corina,
absolut kein Problem, richtig gedacht!! Und ein r=0.89 klingt nach einem guten Ergebnis, gratuliere! Viel Erfolg bei deiner Arbeit!
Liebe Grüße
Ramona
Hallo Alex,
vielen Dank für deine tolle Erklärung!!
Ich bin gerade dabei meine Daten für meine Abschlussarbeit auszuwerten und hänge jetzt an den Korrelationen.
Folgendes Problem:
Für meinen Fragebogen habe ich die Antworten für die Items mit 0, 1 und 2 codiert. Jetzt gibt es aber Versuchspersonen, bei denen der Mittelwert genauso groß wie die einzelnen Elemente ist. Also wenn die Versuchsperson beispielsweise immer 0 angekreuzt hat. Der Nenner ist dadurch = 0 und ich erhalte keinen Korrelationswert.
Es wäre großartig, wenn du ein bisschen Ordnung in mein Wirrwarr bringen könntest!!
Der Nenner ist nur dann null wenn alle Elemente von x genau dem Mittelwert von x sind, und alle Elemente von y genau dem Mittelwert von y sind. In der Situation gibt es keine Korrelation, genau =)
Hallo Alex,
danke für deine Erklärung zu Korrelation. Das ist mir soweit klar. Was ich nicht verstehe, ist der Zusammenhang mit der Signifikanz. Ich habe meine Items korreliert und komme beispielsweise bei der Korrelation auf einen Wert von 0.437 . Mein Programm zeigt mir diesen Wert als 2-seitig signifikant bei einem Niveau von 0,05 an. Ich dachte alles erst über 0 .5 gilt als signifikant.
LG Beate
Hallo,
du verwechselt die Korrelation mit dem p-Wert. Der p-Wert gibt Signifikanz an, wenn er kleiner als 0.05 ist. Die Korrelation kann dagegen irgendeinen anderen Wert haben.
VG,
Alex
Hi Alex,
super Info, herzlichen Dank. Danach habe ich meine Auswertung mit r-Korrelationen gerechnet..
Eine Frage habe ich nun:
Für meine Auswertung habe ich verschiedene Items / Fragen (die auf 5-stufigen Likertskalen beantwortet wurden) anhand der Mittelwerte zusammengefasst und mit Excel die r-Korrelationen errechnet.
In einem Fall ist folgendes passiert:
Bei der Zusammenfassung von 7 Items und dem Abgleich mit einer anderen Kategorie (nennen wir sie IM) kommt r = 0,63 raus.
Dann habe ich diese 7 Items aufgesplittet, um einen Aspekt besonders zu beleuchten und folgendes ist passiert: Bei der Zusammenfassung von 6 der 7 Fragen und dem Abgleich mit der Kategorie IM habe ich als Ergebnis r = 0,62. Die 7. Frage dann im Abgleich mit IM bringt als Ergebnis r = 0,49.
Somit sind die beiden r-Werte beim getrennten Betrachten der einzelnen Items niedriger als der r-Wert für die gesamte Kategorie.
Also nochmal in Kurzform:
Fragen 1-7 und Abgleich mit IM: r = 0,63
Fragen 1-6 und Abgleich mit IM: r = 0,62
Frage 7 und Abgleich mit IM: r = 0,49
Ist das möglich??
Oder habe ich irgendwo einen Fehler eingebaut (habe alles angesucht, aber nichts entdeckt..).
Für deine Hilfe wäre ich seehr dankbar, weiß nämlich nicht, wer das sonst wissen könnte..
LG Anna
Hi Anna,
das kann vorkommen, ja. Besonders wenn zwei Fragen negativ korreliert sind. Schau dir mal die folgenden Daten an:
Da kannst du dir x1 als Frage 1-6 vorstellen. Und x2 als Frage 7. Dann ist x = x1 + x2, also Frage 1-7. Und x ist mit y perfekt korreliert, sehr hoch. Die anderen jeweils niedriger.
VG,
Alex
Hi Alex,
vielen herzlichen Dank für deine schnelle Antwort!
Nun ist es mir klarer und ich kann meine Daten mit gutem Gewissen verwenden.
LG Anna
Der Wert der nachher rauskommt, kann der als Prozentwert angesehen werden? Also 74 % negativer linearer Zusammenhang zwischen den beiden Variablen? …Ich hatte irgendwo in einem Text gelesen „es wurde ein positiver Zusammenhang von 84 % zwischen X und Y festgestellt“, wo auch die Korrelationsanalyse nach Pearson angewendet wurde. Richig so? (Sorry falls das eine etwas doofe Frage ist 😉 )
Hm, theoretisch könnte man das, aber ich hab es so noch nie gesehen. Ich würde sie einfach als Zahl zwischen 0 und 1 ausdrücken 🙂
Moin Alex,
…als mathematisch leider völlig unbegabter Mensch ist Deine obige Erklärung zumindest eine sehr große Hilfe auf dem Weg meiner Bemühung zum (studiumsmässig gerade notwendigen) ’nachträglichen‘ Begreifen von ‚Statistik‘ im Allgemeinen und des PKKE im Besonderen.
Dafür danke ich Dir von Herzen!
LG aus Hamburg, Nils
Vielen Dank für die tolle Erklärung.
Hallo Alex,
Kann es sein, dass du bei der 7. Person einen Zahlendreher drin hast?
In der Tabelle steht 6 und in der Rechnung verwendest du 8…?
LG Lisa
Hi, da habe ich in der Formel tatsächlich ein paarmal 8 statt 6 hingeschrieben.
Die Ergebnisse haben aber trotzdem alle gestimmt – ich habe die Fehler gerade korrigiert.
Vielen Dank für den Hinweis! 🙂
– Alex
Hallo,
du hast mir mit diesem Blogbeitrag wahrscheinlich mein Studium gerettet. Zum ersten Mal habe ich kapiert wie man den Korrelationskoeffizient ausrechnet. Vorher waren das alles nur komische Formeln und jetzt ist es alles so klar.
Danke!
Hallo
Sag mal führst du den Block noch? wenn ja wann kann man mit zweidimensionalen bzw mehrdimensionalen Verteilungsfunktionen rechnen?
Sie stehen im Register aber man kann nicht anklicken
Schon mal vor ab sehr gut gemachter Block!!!!
Vielen Dank
Hi Manuel,
ja, ich bin noch dran. Zweidimensionale Verteilungen habe ich im Moment nicht geplant, ich würde erst die Basics fertigstellen wollen 🙂
Grüße,
Alex