Zwischen einem reinem Zusammenhang, d.h. einer Korrelation zwischen zwei Variablen, und einer tatsächlichen Auswirkung von einer auf die andere Variable, d.h. einer Kausalität, besteht noch ein großer Unterschied, der in diesem Artikel behandelt wird.
Sehen wir uns eine Grafik dazu an. Wir befragen \(n=30\) Personen zu ihrer Schuhgröße und ihrem monatlichem Einkommen.
Wir sehen einen Zusammenhang zwischen den beiden Variablen, der auch tatsächlich vorhanden ist, und durch den Korrelationskoeffizienten \(r\) berechnet werden kann. Es wäre jetzt aber falsch, deswegen auch auf eine Auswirkung von einer der beiden Variablen auf die andere zu schließen.
Einen Korrelation (oder einen Zusammenhang) formuliert man so: „Menschen mit größerer Schuhgröße haben tendenziell ein höheres Einkommen“.
Eine Kausalität würde aber so formuliert werden: „Die Schuhgröße hat einen Einfluss auf das Nettoeinkommen“.
Wenn der zweite Satz stimmen würde, dann könnte man sich morgen Schuhe der Größe 65 kaufen, und bekäme deswegen eine saftige Gehaltserhöhung. Das macht natürlich keinen Sinn. Auch umgekehrt wäre eine Kausalität sinnlos, denn dann hätte das Einkommen eine Auswirkung auf die Schuhgröße. Wenn ich also eine Gehaltserhöhung bekäme, würden deswegen meine Füße wachsen.
Eine Korrelation zwischen zwei Merkmalen \(X\) und \(Y\) bedeutet also noch nicht, dass \(Y\) ein Verursacher von \(X\) ist (oder \(X\) ein Verursacher von \(Y\)). Dieses Phänomen nennt man Scheinkorrelation.
Viele, teils richtig absurde Korrelationen gibt es auf der Webseite „Spurious Correlations“.
Was allerdings hier wahr ist: Wenn man zwei Menschen mit unbekanntem Einkommen auf einem Blatt Papier stehen hat, und einer eine viel größere Schuhgröße hat, erwarten wir von dieser Person ein höheres Einkommen als von der anderen.
Mediator-/Confoundervariablen
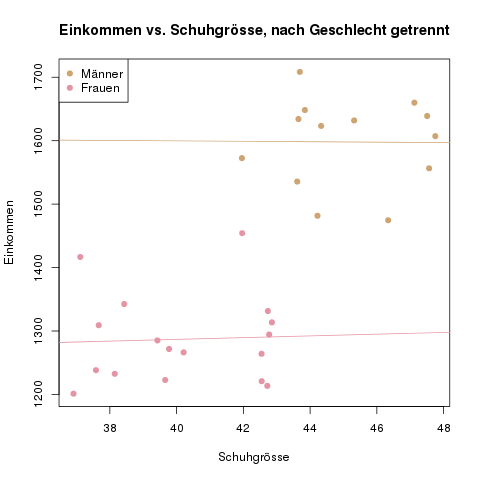
Wer aufgepasst hat, weiss vielleicht schon, was hier vor sich geht: Wir haben eine wichtige Variable, nämlich das Geschlecht der Personen nicht beachtet. Es ist nun so, dass Frauen im Durchschnitt 22% weniger verdienen als Männer. Das hat ein paar erklärbare Gründe, wie z.B. die Tendenz, dass Frauen häufiger Teilzeitjobs oder schlechter bezahlte Berufe annehmen, und ihnen eine steile Karriere nicht so wichtig ist wie z.B. geistige Gesundheit. Aber der Effekt auf das Einkommen ist trotzdem da. Wenn wir unsere befragten Personen nun nach Geschlecht auftrennen, erkennen wir zwei Gruppen, nämlich eine mit großen Füßen und eine mit kleinen Füßen, in denen jeweils keine Korrelation besteht:
Die zu Beginn ignorierte Variable „Geschlecht“ ist hier eine Mediator- oder Confoundervariable (die Worte bedeuten das gleiche, aber in gewissen Fachbereichen benutzt man eines lieber als das andere).
Beispiel aus der Realität
Das klingt nun vielleicht alles etwas realitätsfern, weil mein Beispiel sehr offensichtlich unklug war. Solche Sachen passieren allerdings in der Realität, und auch unter Experten:
Im New England Journal of Medicine, einer hoch angesehenen wissenschaftlichen Zeitschrift, wurde 2012 ein Artikel veröffentlicht, der genau diesen Fehler machte. Sie fanden eine Korrelation zwischen Schokoladenkonsum und Anzahl an Nobelpreisträgern in einem Land, und schlossen auf einen Einfluss von Schokolade auf Intelligenz.
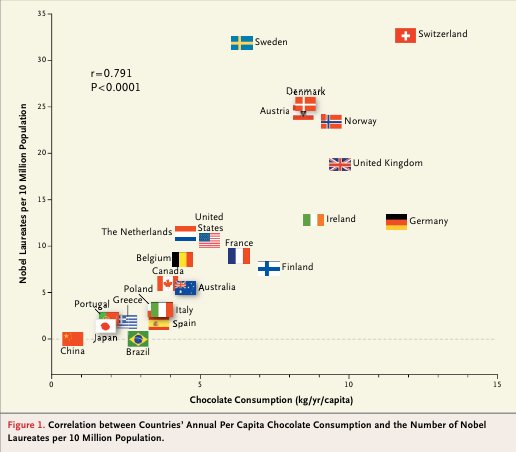
Quelle: Messerli, Franz H. (2012). Chocolate Consumption, Cognitive Function, and Nobel Laureates. New England Journal of Medicine, 367:16, 1562-1564.
Ein Blogartikel, der dieses Beispiel (auf Englisch) ausführlich behandelt, und sich am Ende sogar darüber lustig macht, ist hier zu finden.
Kausalität nachweisen
Wie man sieht, gibt es mehrere mögliche Erklärungen für eine Korrelation zwischen zwei Variablen \(X\) und \(Y\). Es könnte z.B. \(X\) eine Auswirkung auf \(Y\) haben, oder umgekehrt \(Y\) eine Auswirkung auf \(X\), oder aber wie im Beispiel oben eine Mediatorvariable im Spiel sein, die beide Variablen, \(X\) sowie \(Y\) beeinflusst.
Nachweisen kann man eine Kausalität nur durch ein Experiment. Hier müssten wir zum Beispiel von 100 Personen die Schuhgrösse und das Einkommen notieren, und dann der einen Hälfte größere Schuhe geben und der anderen nicht. Wenn sich nun das Einkommen der Treatment-Gruppe, also der Personen mit größeren Schuhen, gegenüber der Kontrollgruppe erhöht, dann haben wir einen Zusammenhang nachgewiesen (das wird aber in diesem Fall eher nicht erwartet).

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!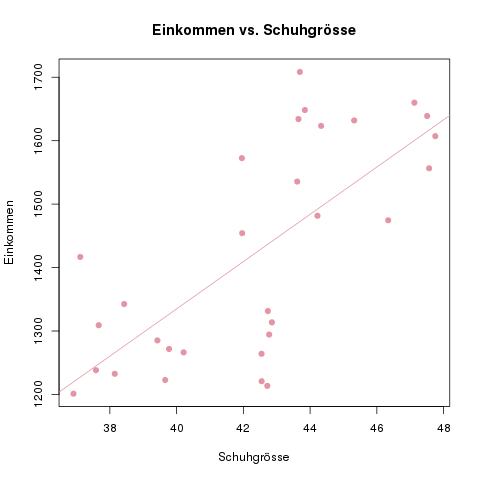
Pingback: Datenmanipulation ade (Teil 2) – Diagramme richtig interpretieren und manipulierte Daten enttarnen - Business -Software- und IT-Blog - Wir gestalten digitale Wertschöpfung
Hallo Alex!
Sehr interessanter Beitrag. Ich habe mich gefragt, wie du an die Daten für den Graphen Einkommen vs. Schuhgröße gekommen bist. Ich möchte auch ein paar Korrelationen erstellen (gerade im Bereich Gesundheit wird ja oft eine Kausalität angenommen, wo keine ist) und dafür brauche ich natürlich Rohdaten. Hast du da einen Tipp?
Lg Antonie
Hi Antonie,
die Daten habe ich frei erfunden, nur zu Illustrationszwecken 🙂
Wenn du nach „practice data sets“ googelst, findest du einige Seiten die Datensätze zur Verfügung stellen.
Eine schöne Seite finde ich die hier: https://www.openml.org/search?type=data
Viele Grüße,
Alex
Pingback: Vitamin D und Covid-19 | gwup | die skeptiker
Pingback: Die 5 größten Mythen in der Ernährung - und wo sie herkommen
Lieber Alex
Ich versuche den Einfluss von Persönlichkeitsmerkmalen auf das langfristige Arbeitserleben bei Lehrpersonen zu untersuchen.
Ich habe nun beispielsweise eine Korrelation zwischen dem Persönlichkeitsmerkmal X und einem hohen Burnout-Wert gefunden. Ist es korrekt, dass ich die Kausalität bei diesem Beispiel gar nie beweisen kann? Oder hilft beispielsweise eine multiple Regressionsanalyse, bei der Alter, Schulstufe und Geschlecht miteinbezogen werden?
Vielen Dank für deine Hilfe.
Hallo Jasmin,
mit 100% Sicherheit kann man eine Kausalität soweit ich weiß nicht nachweisen. Dazu müsstest du dir sicher sein, alle möglichen Mediatoren (z.B. Alter, Schulstufe, Geschlecht, …) erkannt und aufgenommen zu haben.
Es gibt hier einen Blogartikel, in dem ein paar Kriterien gelistet sind, die eine Kausalität wahrscheinlicher machen: https://statswithcats.wordpress.com/2015/01/01/how-to-tell-if-correlation-implies-causation/
Man kann also Hinweise (oder starke Hinweise) auf eine Kausalität entdecken, wenn man sorgfältig Mediatoren auswählt, und es z.B. keine andere bessere Erklärung für einen Zusammenhang gibt. Aber man kann es nie ganz ausschließen, dass die Korrelation doch einen anderen Grund hat.
Viele Grüße,
Alex
Hi!
Ich hoffe, ich bin hier richtig mit meiner Frage.
Welchen Test muss ich denn nehmen, um z.B. die Dauer der Gabe eines Medikaments mit den Auswirkungen auf verschiedene Parameter zu unterschiedlichen Zeitpunkten herauszufinden, bzw. ob das korreliert?
Beispiel:
Z.B. Dauer der Gabe des Medikaments mit den Erythrozytenzahlen an Tag 1 und den Erythrozytenzahlen an Tag 7? Muss ich dafür ne Rangfolge erstellen, oder wie kriege ich das hin, da es ja quasi ein Verlauf ist..bin maßlos überfordert..
Aber vielen Dank schonmal vorab:)
Hi,
das kommt ganz auf das Skalenniveau deiner Variablen an. Ich habe hier einen Artikel dazu geschrieben: https://www.crashkurs-statistik.de/welchen-statistischen-test-soll-ich-waehlen/
VG
Alex
Ein sehr interessanter Beitrag! Dazu eine Frage aus meiner beruflichen Praxis:
Ich bin Agrarwissenschaftler und Tierernährer. Ich bin fest davon überzeugt, dass wir durch die Zucht der landwirtschaftlichen Nutztiere diese längst physiologisch überfordern mit der Folge, dass die Tiere früher ausscheiden, nicht mehr so lange genutzt werden können, die Nutzungsdauer sinkt. I.Ü. sind sie mehr unterschwellig krank. Tierwohl etc. Nun halten mir die Züchter und auch andere Experten, die anderer Meinung sind (ich nenne sie: Hardcore Züchter) entgegen: „Ich zeige Ihnen jede Menge Betriebe, die haben sehr hohe Leistungen und die Kühe werden sehr alt.“ Dem hat ein Wissenschaftler mal entgegnet: „Das ist ein induktiver Fehlschluss!“ Ich glaube, dass ich das inzwischen verstanden habe und dass das auch so ist. Die Züchter sagen aber auch: „Wir können keine Korrelation zwischen Leistung und Gesundheit feststellen.“ Nach dem, was ich jetzt über den Zusammenhang Korrelation – Kausalität gelesen habe, frage ich mich jetzt: „Ist denn eine Korrelation überhaupt erforderlich, um einen kausalen Zusammenhang zu begünden? Oder kann ein Zusammnmenhang kausal sehr wohl begündet werden, ohne dass eine Korrelation besteht?“
Besten Dank und viele Grüße
Hallo Herr Menn,
es gibt Zusammenhänge, die nicht linear sind – dort wäre es denkbar, dass es Situationen gibt, in denen die Korrelation nahe an 0 ist, aber trotzdem ein kausaler Zusammenhang besteht.
In den meisten Fällen, wenn nämlich ein linearer Zusammenhang unterstellt wird, ist eine Korrelation allerdings Voraussetzung für einen kausalen Zusammenhang. Dann wird der Zusammenhang ja ausgedrückt in Sätzen wie „wenn X ansteigt, dann steigt auch Y an“.
Viele Grüße
Hallo Alex,
herzlichen Dank für deine Antwort. Die hilft mir weiter. Denn selbstverständlich ist der Zuzsammenhang zwischen Leistungssteigerung (immer mehr Milch pro Kuh und Jahr) und Gesundheit, Fitness usw. nicht linear, jedenfalls kann ich mir das nicht vorstellen. Somit schließe ich, dass sehr wohl ein Zusammenhang bestehen kann, obwohl die Korrelation nahe 0 oder nicht feststellbar ist.
Physiologisch lässt sich der Zusammenhang jedenfalls begründen.
Nochmals danke u. viele Grüße
Frank
Pingback: Richtig wissenschaftlich arbeiten - Recherchieren, Planen und Umsetzen
Pingback: MS Stiftung Trier
Danke für diesen einleuchtenden Beitrag zu einem wichtigen statistischen Thema.
Mir ist jedoch ein gravierender Fehler in Ihrem Beitrag aufgefallen:
„Es ist nun so, dass Frauen im Durchschnitt 22% weniger verdienen als Männer. Das hat ein paar erklärbare Gründe, wie z.B. die Tendenz, dass Frauen häufiger Teilzeitjobs oder schlechter bezahlte Berufe annehmen, und ihnen eine steile Karriere nicht so wichtig ist wie mehr Freizeit.“.
Insbesondere, der letzte Grund ist sicherlich keine valide Erklärung für den Fakt, dass Frauen ca. 22% weniger verdienen als Männer. Ich empfehle Basisliteratur zur Gender Pay Gap und der sogenannten unbezahlten Care-Arbeit (dies v.a. bzgl. sogenannter „Freizeit“).
Viele Grüße
Uff, ja, schwieriges Thema. Für das Einlesen in Basisliteratur fehlt mir leider die Zeit 🙂
Mein Hauptpunkt ist, dass vieles aus frei treffbaren Entscheidungen folgt, nicht aus einer Geschlechterdiskriminierung. Verschiedene Studiengänge führen zu verschiedenen Berufsgruppen. Als Beispiel würde ich da mal das Geschlechterverhältnis im Soziologiestudium und das in Ingenieursstudiengängen angeben. Ingenieure sind tendenziell besser bezahlt als z.B. Erzieher. Den Studiengang kann man aber im Vorfeld sicherlich frei wählen. Ein Kind großzuziehen, und Care-Arbeit, so edel sie ist, ist ebenso eine freie Wahl (Vorsicht: Möchte ich hier nicht abwerten, sondern nur als freie Wahl darstellen).
Ein Punkt noch von der anderen Seite: Es sind etwa 94% aller Gefängnisinsassen Männer. Da beschwert sich keiner über Diskriminierung der Gerichte, sondern der Grund ist klar: Wir sind im Mittelwert (!) aggressiver, gewalttätiger, risikofreudiger. Deswegen gehe ich aber nicht auf die Straße und fordere ein Ende der Diskriminierung. Stattdessen verkloppe ich einfach keine Leute und zahle brav meine Steuern. Das ist meine Entscheidung 🙂 Die Ungleichheit der Geschlechter im Gefängnis wird man wohl nie auf 50/50 „korrigieren“ können. Das heißt aber nicht, dass der einzelne immer noch selbst entscheiden kann, welchen Weg er geht.
Kriminell oder gesetzestreu.
Soziologie oder Maschinenbau.
Do what you want 🙂
Auf dem Punkt gebracht !
Pingback: Ein "stichhaltiges" #Argument für die Abtreibung - oder auch nicht - pelzblog
Pingback: EIKE in ARD-Beitrag „Klimareport“: Temperatur nicht nennenswert gestiegen – keine Beweise für menschengemachten Klimawandel – Gegen den Strom
Pingback: Medizin. Wissenschaft - Fehler in Design / Auswertung von Studien - Seite 9
Pingback: Sind "psychische Krankheiten" objektivierbar? Thomas Insel NIMH - Seite 17
Pingback: Korrelation und Kausalität: Wieso Nicolas Cage (keine) Menschen ertränkt - KulturData
Ein hoch-notwendiger Beitrag mit drastischen, unmittelbar einleuchtenden Beispielen! Leider ist der Schluss von einer Korrelation auf eine Kausalität ungeheuer (!) weit verbreitet, leider auch in der „wissenschaftlichen“ Literatur, und – wenn der Unsinn nicht so augenfällig ist – fällt man bereitwillig darauf herein: Fettkonsum -> Adipositas, Sport -> Gesundheit u.v.m.
Meist liegt auch eine Missachtung des Prinzips des „ceteris paribus“ vor.
Warum werden so oft gigantisch teuere „Studien“ durchgeführt, gelegentlich auch noch von Interessenvertretern gesponsort, statt sich z.B. mit den bekannten biochemischen, physiologischen u.a. Zusammenhängen zu beschäftigen?
Pingback: “Die Berechnung der Welt”, ein Buch zu einem komplexen Thema von Klaus Mainzer | das Informatische und die Bildung
Sehr gut erklärt, vielen Dank!
Pingback: Impfen bei Lesch und in den Medien: “Wir merken nicht, dass Impfungen uns schützen“ @ gwup | die skeptiker