Das Wichtigste in Kürze
Lageparameter beschreiben grob gesagt, wo auf einer Skala sich die Daten befinden. Dabei gibt es verschiedene Methoden der Berechnung, die für verschiedene Merkmalstypen mehr oder weniger Sinn machen. Eine kurze Übersicht sieht man in der Tabelle unten. Da der Median ein bestimmtes Quantil ist (nämlich das 50%-Quantil), sind die beiden Spalten gleich. Mit „Diskret“ sind in dieser Tabelle Zähldaten wie etwa die Kinderzahl gemeint.
| Modus | Median | Quantile | Mittelwert | |
|---|---|---|---|---|
| Nominal | ja | nein | nein | nein |
| Ordinal | ja | ja | ja | nein |
| Diskret | ja | ja | ja | ja |
| Stetig klassiert | ja | ja | ja | nein |
| Stetig | nein | ja | ja | ja |
Arithmetischer Mittelwert
Der arithmetische Mittelwert (oft auch „arithmetisches Mittel“ oder nur „Mittelwert“ genannt) ist der bekannteste Lageparameter. Er wird gebildet, indem man alle Ausprägungen aufsummiert und durch die Gesamtzahl von Ausprägungen teilt. Für die Beobachtungen \(x_1, x_2, \ldots, x_n\) sieht das arithmetische Mittel \(\bar{x}\) folgendermaßen aus:
\[ \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i \]
Angenommen, wir befragen 7 Familien nach der Kinderzahl im Haushalt und bekommen folgende Antworten:
| Familie | Weber | Kaiser | Kandl | Nöbauer | Sturm | Baumann | Dürr |
|---|---|---|---|---|---|---|---|
| Merkmal | \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | \(x_5\) | \(x_6\) | \(x_7\) |
| Kinder | 1 | 2 | 6 | 1 | 1 | 3 | 2 |
Der Mittelwert berechnet sich demnach zu \(\frac{1}{7}(1+2+6+1+1+3+2) = 2.2857\).
Median
Der Median ist der Wert, der die Daten in zwei gleich große Hälften teilt. Genauer gesagt ist es der Wert, für den mindestens die Hälfte der Daten kleiner oder gleich dem Median, und mindestens die Hälfte der Daten größer oder gleich dem Median sind. Warum man das so kompliziert formulieren muss, sehen wir gleich am folgenden Beispiel.
Schauen wir uns nochmal die Kinderzahlen an, um die es beim arithmetischen Mittel schon ging. Um für diese Daten den Median von Hand zu bestimmen, müssen wir die Merkmalsausprägungen zuerst aufsteigend in eine sogenannte geordnete Urliste sortieren:
| Merkmal | \(x_{(1)}\) | \(x_{(2)}\) | \(x_{(3)}\) | \(x_{(4)}\) | \(x_{(5)}\) | \(x_{(6)}\) | \(x_{(7)}\) |
|---|---|---|---|---|---|---|---|
| Kinder | 1 | 1 | 1 | 2 | 2 | 3 | 6 |
Wenn der Index—wie hier—in Klammern steht, handelt es sich immer um sortierte Daten.
Nun brauchen wir eine Zahl (das muss, genau wie beim Mittelwert, nicht unbedingt eine Merkmalsausprägung aus der Datenreihe sein), für die mindestens die Hälfte der Daten größer/gleich diesem Wert sind, und mindestens die Hälfte kleiner/gleich.
Würden wir die Zahl 1 nehmen, sind \(\frac{3}{7}\), also ca. 43% der Daten kleiner/gleich der 1, und 100% der Daten größer/gleich der 1. Hätten wir z.B. die Zahl 1.5 gewählt, wären immer noch 43% der Daten kleiner/gleich der 1.5, aber jetzt sind nur noch \(\frac{4}{7}\), also ca. 57\% der Daten größer/gleich der 1.5. Nehmen wir jetzt die Zahl 2 als möglichen Median. Es sind nun \(\frac{5}{7}\), also ca 71% kleiner/gleich der 2, und \(\frac{4}{7}\), also ca. 57% größer/gleich der 2. Wir haben unseren Median gefunden.
Der Median ist übrigens ein robuster Lageparameter, da er auf Ausreißer in den Daten nicht so stark reagiert wie z.B. der Mittelwert. Falls die Familie Kandl einen unerwarteten Kinderschub bekommt, könnte unsere Urliste auf einmal wie folgt aussehen:
| Merkmal | \(x_{(1)}\) | \(x_{(2)}\) | \(x_{(3)}\) | \(x_{(4)}\) | \(x_{(5)}\) | \(x_{(6)}\) | \(x_{(7)}\) |
|---|---|---|---|---|---|---|---|
| Kinder | 1 | 1 | 1 | 2 | 2 | 3 | 127 |
Das ist natürlich eine etwas optimistische Kinderplanung. Aber der wichtige Punkt ist dieser: Der Mittelwert ist jetzt 19.57, aber der Median ist immer noch 2.
Mit Hilfe der Schreibweise \(x_{(i)}\) für sortierte Daten lässt sich der Median nun sehr leicht mathematisch hinschreiben:
\[ x_\mathrm{med} = \begin{cases} x_{(\frac{n+1}{2})} & n \text{ ungerade}\\ \frac{1}{2} (x_{(\frac{n}{2})} + x_{(\frac{n}{2}+1)}) & n \text{ gerade} \end{cases} \]
Die zweiteilige Definition ist deswegen notwendig, weil wir bei einer ungeraden Anzahl von Daten einfach den „mittleren“ Datenpunkt nehmen können—bei fünf Datenpunkten also einfach den dritten (die Grafik unten klärt das vielleicht). Falls wir eine gerade Anzahl von Datenpunkten (z.B. vier) haben, gibt es keinen direkten „mittleren“ Punkt, und wir müssen den Mittelwert aus den „beiden mittleren“ (z.B. dem zweiten und dritten Punkt) bilden.
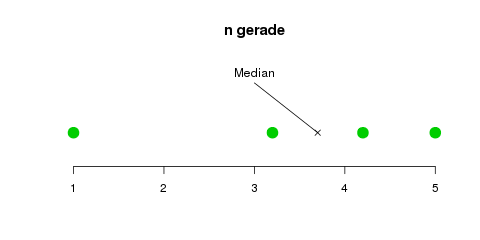
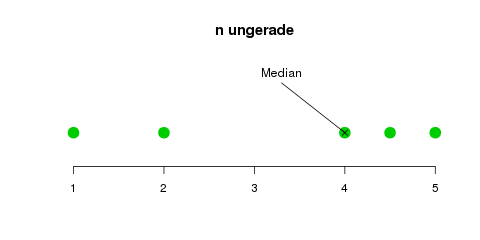
Der Median einer Datenreihe mit einer ungeraden bzw. geraden Anzahl von Elementen. Bei einer ungeraden Anzahl gibt es ein „mittleres“ Element, nämlich das \(\frac{n+1}{2}\)-te Element \(x_{(\frac{n+1}{2})}\). Bei einer geraden Anzahl bildet man den Mittelwert zwischen den zwei Elementen in der Mitte, dem \(\frac{n}{2}\)-ten und dem \((\frac{n}{2}+1)\)-ten Element: \(\frac{1}{2}(x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)})\)
Modus
Der Modus oder Modalwert ist nur für nicht-stetige Daten definiert. Er ist die Ausprägung, die in der Stichprobe am häufigsten gezählt wurde. Für unsere Stichprobe zur Kinderanzahl ist der Modus also 1, da drei Familien ein Kind haben. Kein allzu großes Geheimnis.
Beispielaufgabe
Schauen wir uns Beispieldaten eines diskreten Merkmals für 7 Personen an. Wir berechnen für diese Datenreihe den Mittelwert, Median, Modus, und das 75%-Quantil.
| Person | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Merkmal | 3 | 2 | 0 | 5 | 1 | 4 | 4 |
Der Mittelwert berechnet sich zu \(\frac{1}{7}(3+2+0+5+1+4+4) \approx 2.714\). Für den Median ordnen wir unsere Daten. Da \(n\) ungerade ist, können wir direkt das mittlere, vierte Element in der geordneten Liste verwenden:
| geordnetes Merkmal | 0 | 1 | 2 | 3 | 4 | 4 | 5 |
|---|
Der Median ist also 3. Der Modus ist 4, da diese Ausprägung am häufigsten (zweimal) vorkommt.
Zum 75%-Quantil: Wir wollen also einen Wert bestimmen, der die Daten so aufteilt, dass mindestens 75% kleiner/gleich und mindestens 25% größer/gleich diesem Wert sind. Diese Datenreihe kann man nicht genau in 75% und 25% aufteilen, d.h. \(np\) ist keine ganze Zahl. Über die Formel \(x_{(\lfloor np \rfloor + 1)}\) kommen wir zu \(x_{(5+1)}\), also dem sechsten Wert in der geordneten Liste, nämlich 4.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hallo,
ich hätte eine Frage zum Median. Du hast es wirklich toll erklärt und ich verstehe auch wieso er im Beispiel zwei ist, aber ich verstehe nicht wie man die Formel anwenden soll? Tut mir leid, falls ich mich gerade wirklich doof anstelle. Aber wenn man 100 Daten hat kann man die ja nicht alle sortieren. Könntest du das Beispiel bitte mal in die Formel einsetzen?
Danke im Voraus!
Annika
Doch, du musst in dem Fall alle 100 Daten sortieren, und dann den Mittelwert zwischen Platz 50 und Platz 51 nehmen 🙂
Das heißt man muss es immer von Hand machen und kann keine Formel verwenden?
Naja, die Formel ist oben gegeben, aber du musst sie in einer Klausur von Hand ausrechnen. Das ist aber beim Mittelwert genauso.
In der Realität macht das natürlich der Computer, dann passiert nichts mehr von Hand.
Hi Alex,
kann man denn auch bei qualitativen nominalen Merkmalen wie zB „normal, gut, sehr gut“ den Median und die Quartile, bei insgesamt n=18 Beobachtungen bei denen 7 mal “normal“, 10 mal „gut“ und ein mal „sehr gut“ vorkommt, berechnen?
Für eine Antwort wäre ich dir sehr dankbar
VG
Hi Felix,
das kann man, ja – du musst die Ausprägungen einfach aufsteigend sortieren und dann so vorgehen wie hier im Artikel beschrieben.
Viele Grüße,
Alex
Hallo Alex,
erst einmal vielen Dank für diese Seite! Mein letzter Matheunterricht war vor 6 Jahre der Grundkurs in der Schule, da lässt mich Statistik in der Uni ehrlich gesagt derzeit ziemlich verzweifeln.
Kann es sein, dass sich in der Beispielaufgabe bei der Berechnung des Mittelwerts ein Tippfehler eingeschlichen hat? Ich glaube es müsste 1/7 * (3+2+0+5+1+4+4) heißen, oder?
Liebe Grüße,
Jane
Hi Jane,
ja, da habe ich mich wohl wirklich vertippt. Der Mittelwert selber hat aber gepasst… naja.
Danke für den Hinweis! Ich hab’s gerade korrigiert 🙂
– Alex
Hallo,
Ich habe eine Frage zum Modus. Es wurde in vorlesung gesagt dass, der Modus einer Datenreihe das Merkmal bzw. der Wert mit der größten Häufigkeit ist. Wäre das nicht im Beispieleaufgabe „5“.
Also ich habe meinem Tutor die Aufgabe gezeigt und der meinte, es wäre „5“.
bin schon verwirrt. hilfe bitte.
Gruß daniele,
Aber in der Beispielaufgabe kommt die 5 nur einmal vor, und die 4 zweimal.
Daher ist der Modus 4.
Beantwortet das deine Frage?
Viele Grüße,
Alex
Hey Alex, vielen Dank für dein Wissen, dass du allen auf dieser Webside kostenlos zur Verfügung stellst. Ich freue mich sehr diese Internetseite gefunden zu haben.
Kannst du vielleicht den Unterschied zwischen „stetig“ und „stetig klassiert“ erläutern? Der Begriff „stetig klassiert“ taucht im Abschnitt „Merkmalstypen: Diskrete und stetige Merkmale“ nicht auf.
Stimmt, das muss ich tatsächlich noch ergänzen. Ganz kurz: Wenn ich stetige Daten, z.B. die Körpergrösse, in beliebige Gruppen/Klassen aufteile (sagen wir „unter 150cm“, „150-180cm“, und „über 180cm“), dann kannst du diese klassierten Daten behandeln wie ordinale Daten.
Ich hoffe das hilft dir schon weiter.
VG,
Alex
Zum Median heisst es: „das muss, genau wie beim Mittelwert, nicht unbedingt eine Merkmalsausprägung aus der Datenreihe sein“. Später wird jedoch gezeigt, wie der Wert aus bestehenden Merkmalen einer gerade bzw. ungeraden sortierten Reihe ausgewählt wird. Ein Widerspruch, oder?
Im Falle von „\(n\) gerade“ nimmt man den Wert zwischen den beiden „mittleren“ Ausprägungen, das ist dann dieser Spezialfall, den ich meinte.
Falls \(n\) ungerade ist, nimmt man natürlich einen Wert aus den Daten.
Hallo,
in der Beispielaufgabe wird das 75% Quantil widersprüchlich zum Kapitel Quantile erklärt. Hier wird gesagt das 75% der Daten größer/gleich dem Wert seien sollen und 25% kleiner/gleich. Dies umschreibt meines Erachtens das 25% Quantil. Die anschließende Beispielrechnung gehört wiederum zum 75 % Quantil. Zur Korrektur sollten lediglich das größer und kleiner vertauscht werden.
Gruß Dustin
PS: Danke nochmals für die anschaulichen und leicht verdaulichen Informationen. Super um wieder in die Thematik einzufinden!
Danke auch für diesen Hinweis!
Viel Spaß noch beim Lesen,
Alex
danke alex
liebe gruß svea