t-Verteilung: Stichprobenmittelwerte

Idee

Die \(t\)-Verteilung wird insbesondere für Hypothesentests und Konfidenzintervalle benötigt. In beiden Situationen interessiert uns nämlich die Verteilung des Stichprobenmittelwerts.

Und falls die wahre Varianz \(\sigma^2\) der Daten nicht bekannt ist, d.h. man stattdessen die Stichprobenvarianz \(s^2\) berechnen muss (und das ist in der Realität quasi immer so), ist der Mittelwert der Stichprobe nämlich nicht normalverteilt, sondern \(t\)-verteilt mit \(n-1\) Freiheitsgraden.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Wenn ich also aus einer großen Grundgesamtheit (mit Mittelwert 0) für 365 Tage lang jeden Tag eine Stichprobe der Größe \(n=30\) ziehe, und dann den Mittelwert daraus bilde, folgen die so bestimmten 365 Mittelwerte einer \(t\)-Verteilung mit \(n-1=29\) Freiheitsgraden. Das Histogramm dieser 365 Datenpunkte läge also sehr nah an dieser theoretischen \(t\)-Verteilung der Daten.

Es gilt dann:

\[ \begin{align*} T &= \frac{\bar{X} – \mu_0}{s} \sqrt{n} \\ T & \sim t(n-1) \end{align*} \]

Die Standardisierung, d.h. das Subtrahieren von \(\mu_0\) und das Teilen durch \(s\), geschieht aus dem Grund, dass die danach erhaltenen Zahlen auf einer einheitlichen Skala leben (man kann sagen: von etwa -3 bis +3), und man dann nur eine einzige Tabelle drucken muss. Wenn man zum Beispiel mit einem Hypothesentest überprüfen möchte, ob die durchschnittliche Körpergrösse bei Männern 175cm ist, dann setzt man \(\mu_0 = 175\). Vom tatsächlichen durchschnittlichen Wert der Stichprobe (z.B. 176.3cm) zieht man nun die postulierten 175cm (also \(\mu_0\)) ab, und teilt durch die berechnete Standardabweichung \(s\) aus der Stichprobe.

Als kurze Anmerkung sei erwähnt, dass für größere Stichproben (Faustregeln sprechen oft von \(n>50\) oder \(df>50\)) statt der \(t\)-Verteilung als Approximation auch die Normalverteilung verwendet werden kann. Die Kurven der Dichte und Verteilungsfunktion der Normalverteilung und \(t\)-Verteilung mit sehr vielen Freiheitsgraden sind nämlich ähnlich genug, dass es fast keinen Unterschied macht, welche man verwendet.

Parameter

Je größer die Stichprobe wird, desto größer wird die Anzahl der Freiheitsgrade, und desto mehr ähnelt die zugehörige \(t\)-Verteilung dann der Normalverteilung. Die folgende Grafik veranschaulicht den Einfluss des Parameters \(df\):

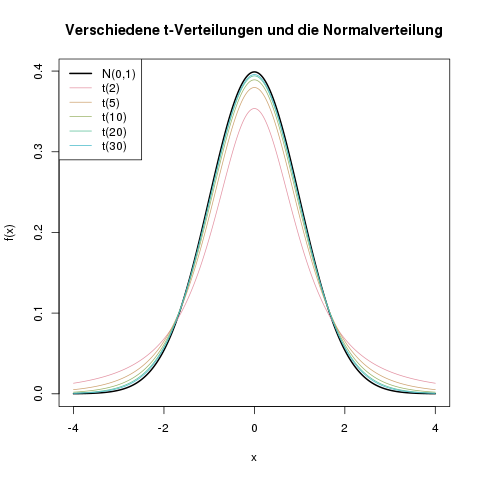
Die \(t\)-Verteilung hat eine breitere Streuung als die Standardnormalverteilung \(N(0,1)\). Mit steigender Anzahl der Freiheitsgrade \(df\) nähert sich die \(t\)-Verteilung aber der Normalverteilungskurve an. Ab etwa \(df=50\) ist sie nah genug an der Normalverteilung, dass man die \(t\)-Verteilung mit ihr approximieren kann.

Je höher also die Anzahl der Freiheitsgrade \(df\), desto ähnlicher ist die \(t\)-Verteilung der Standardnormalverteilung \(N(0,1)\). Ab etwa 50 Freiheitsgraden, also \(df>50\), kann man mit dem Auge fast keinen Unterschied mehr zwischen den beiden Kurven erkennen.

Für eine \(t\)-verteilte Zufallsvariable \(X\) mit \(df\) Freiheitsgraden schreibt man

\[ X \sim t(df) \]

Träger

Die \(t\)-Verteilung geht genauso wie die Normalverteilung über die gesamten reellen Zahlen. Ihr Träger ist also

\[ \mathcal{T} = \mathbb{R} \]

Erwartungswert, Varianz und Dichte

Man benötigt in der Praxis eigentlich nur die Verteilungsfunktion der \(t\)-Verteilung, wie vorher schon erwähnt, um Hypothesentests und Konfidenzintervalle rechnen zu können. Es wird also in der Statistik (und in Klausuren) in den allermeisten Fällen weder die Dichtefunktion, noch Erwartungswert und Varianz vorkommen.

Der Vollständigkeit halber sei aber erwähnt, dass für eine \(t\)-verteilte Zufallsvariable der Erwartungswert \(\mathbb{E}(X) = 0\), und die Varianz \(\mathbb{V}(X) = \frac{df}{df-2}\) ist.

Verteilungsfunktion

Die Verteilungsfunktion (genauso wie die Dichtefunktion) lässt sich nur sehr eklig als Formel notieren. Das Ausrechnen dieser Funktion ist wohl niemandem zuzumuten, weshalb es für die \(t\)-Verteilung auch eine Verteilungstabelle gibt, in der man die wichtigsten Werte nachschlagen kann.

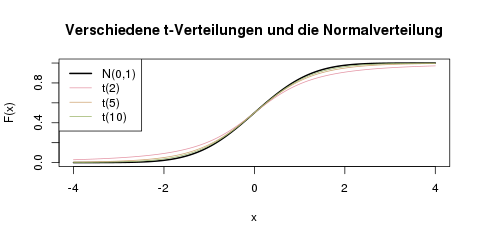
Verteilungsfunktionen für drei ausgewählte \(t\)-Verteilungen. Auch die Verteilungsfunktion ähnelt sich mit steigenden Freiheitsgraden immer mehr der Standardnormalverteilung an.