Wie man die Verteilungstabelle abliest
Weil die Standardnormalverteilung so eine zentrale Rolle spielt (und, damit man sie nicht mit der Verteilungsfunktion von unstandardisierten Zufallsvariablen verwechselt), bekommt diese Verteilung meist einen eigenen Buchstaben, das griechische grosse Phi. Statt \(F(x)\) schreibt man in den meisten Büchern und Vorlesungen dann \(\Phi(z)\), wobei \(z\) für den standardisierten Wert steht.
Um Platz zu sparen, ist in den meisten Büchern und Klausuren nur die rechte Hälfte der Verteilungsfunktion tabelliert.
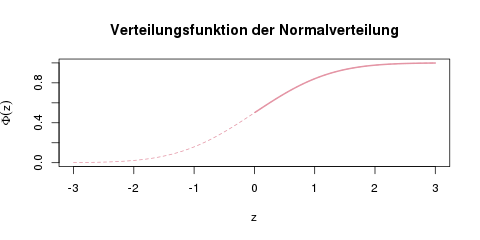
Die Verteilungsfunktion der Normalverteilung. In Tabellen findet man häufig nur die rechte Hälfte dieser Kurve, also ab \(\Phi(0)=0.5\).
Den Wert \(\Phi(z)\) für alle positiven \(z\) kann man nun einfach aus der Tabelle ablesen. Meistens sind die Tabellen so aufgebaut, dass in den Zeilen die ersten beiden Stellen für \(z\) stehen, und in 10 Spalten dann die zweite Nachkommastelle. Aus der Tabelle liest man also z.B. \(\Phi(0.01) = 0.5040\), oder \(\Phi(1.96) = 0.975\).
Um den Wert \(\Phi(z)\) für ein negatives \(z\), zum Beispiel \(\Phi(-1.5)\) zu erhalten, ist dann ein zusätzlicher Rechenschritt nötig, der in der folgenden Grafik erklärt ist.
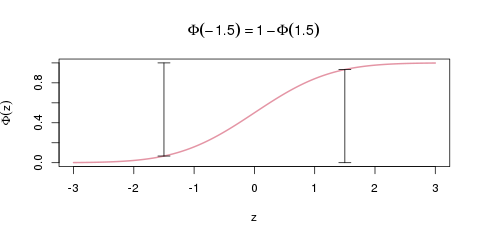
So berechnet man die Verteilungsfunktion an negativen \(x\)-Stellen. Die beiden vertikalen Balken sind genau gleich hoch (nämlich \(\Phi(1.5)=0.93\)).
Da die Verteilungskurve nämlich symmetrisch um den Punkt (0, 0.5) ist, kann man sich dieses Tricks bedienen:
\[\Phi(-z) = 1-\Phi(z) \]
Man berechnet also die Verteilungsfunktion an der Stelle \(-1.5\), indem man den Wert für \(+1.5\) in der Tabelle findet, und ihn von 1 abzieht:
\[\Phi(-1.5) = 1-\Phi(1.5) = 1-0.933 = 0.067 \]
Zwischenaufgabe
Bestimme mit Hilfe der untenstehenden Tabelle \(\Phi(1)\), \(\Phi(-1)\), und \(\Phi(-1.96)\).
Sehr große Zahlen
Für Zahlen, die so groß (oder so klein im Negativen) sind, dass man sie nicht mehr in der Tabelle findet, kann man näherungsweise als Wahrscheinlichkeit „fast Null“ oder „fast Eins“ nehmen. An der Grafik der Verteilung oben kann man intuitiv verstehen, warum das so ist. Die Funktion nähert sich für sehr große Zahlen der 1 an, und für sehr kleine Zahlen der 0.
Als Formel ausgedrückt, falls man z.B: \(\Phi(15)\) berechnen will:
\[\Phi(15) \approx 1\]
\[\Phi(-15) \approx 0\]
Quantile ablesen
Quantile liest man genau andersherum aus der Verteilungstabelle ab, da die Quantilsfunktion ja genau die Umkehrfunktion der Verteilungsfunktion ist.
Wenn man direkt die ersten beiden Zellen der Tabelle betrachtet, ist also das 0.5000-Quantil der Standardnormalverteilung gleich 0.00. Das 0.5040-Quantil ist 0.01, und so weiter. Das 75%-Quantil liegt zwischen 0.67 und 0.68, da \(\Phi(0.67)=0.7486\) ist, und \(\Phi(0.68)=0.7517\).
Für die Quantile unter 50% muss man wieder über einen kurzen Umweg rechnen, da die Tabelle nur positive \(z\), und damit Quantile über 0.5 abbildet.
Für das \(\alpha\)-Quantil gilt: \(q_\alpha = -q_{1-\alpha}\). Das bedeutet: Möchte man das 20%-Quantil bestimmen, sucht man (weil es unter 50% liegt) in der Verteilungstabelle stattdessen das (1-0.2)-Quantil, also das 80%-Quantil, und nimmt den negativen Wert des Ergebnisses. Das 80%-Quantil ist also 0.84, und das 20%-Quantil ist somit -0.84.
Zwischenaufgabe
Bestimme das 97.5%-Quantil sowie das 2.5%-Quantil der Standardnormalverteilung.
Die Tabelle der Standardnormalverteilung
| \(\downarrow\) z-Werte | Zweite Nachkommastelle \(\rightarrow\) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | |
| 0,0 | 0,5000 | 0,5040 | 0,5080 | 0,5120 | 0,5160 | 0,5199 | 0,5239 | 0,5279 | 0,5319 | 0,5359 |
| 0,1 | 0,5398 | 0,5438 | 0,5478 | 0,5517 | 0,5557 | 0,5596 | 0,5636 | 0,5675 | 0,5714 | 0,5753 |
| 0,2 | 0,5793 | 0,5832 | 0,5871 | 0,5910 | 0,5948 | 0,5987 | 0,6026 | 0,6064 | 0,6103 | 0,6141 |
| 0,3 | 0,6179 | 0,6217 | 0,6255 | 0,6293 | 0,6331 | 0,6368 | 0,6406 | 0,6443 | 0,6480 | 0,6517 |
| 0,4 | 0,6554 | 0,6591 | 0,6628 | 0,6664 | 0,6700 | 0,6736 | 0,6772 | 0,6808 | 0,6844 | 0,6879 |
| 0,5 | 0,6915 | 0,6950 | 0,6985 | 0,7019 | 0,7054 | 0,7088 | 0,7123 | 0,7157 | 0,7190 | 0,7224 |
| 0,6 | 0,7257 | 0,7291 | 0,7324 | 0,7357 | 0,7389 | 0,7422 | 0,7454 | 0,7486 | 0,7517 | 0,7549 |
| 0,7 | 0,7580 | 0,7611 | 0,7642 | 0,7673 | 0,7703 | 0,7734 | 0,7764 | 0,7794 | 0,7823 | 0,7852 |
| 0,8 | 0,7881 | 0,7910 | 0,7939 | 0,7967 | 0,7995 | 0,8023 | 0,8051 | 0,8078 | 0,8106 | 0,8133 |
| 0,9 | 0,8159 | 0,8186 | 0,8212 | 0,8238 | 0,8264 | 0,8289 | 0,8315 | 0,8340 | 0,8365 | 0,8389 |
| 1,0 | 0,8413 | 0,8438 | 0,8461 | 0,8485 | 0,8508 | 0,8531 | 0,8554 | 0,8577 | 0,8599 | 0,8621 |
| 1,1 | 0,8643 | 0,8665 | 0,8686 | 0,8708 | 0,8729 | 0,8749 | 0,8770 | 0,8790 | 0,8810 | 0,8830 |
| 1,2 | 0,8849 | 0,8869 | 0,8888 | 0,8907 | 0,8925 | 0,8944 | 0,8962 | 0,8980 | 0,8997 | 0,9015 |
| 1,3 | 0,9032 | 0,9049 | 0,9066 | 0,9082 | 0,9099 | 0,9115 | 0,9131 | 0,9147 | 0,9162 | 0,9177 |
| 1,4 | 0,9192 | 0,9207 | 0,9222 | 0,9236 | 0,9251 | 0,9265 | 0,9279 | 0,9292 | 0,9306 | 0,9319 |
| 1,5 | 0,9332 | 0,9345 | 0,9357 | 0,9370 | 0,9382 | 0,9394 | 0,9406 | 0,9418 | 0,9429 | 0,9441 |
| 1,6 | 0,9452 | 0,9463 | 0,9474 | 0,9484 | 0,9495 | 0,9505 | 0,9515 | 0,9525 | 0,9535 | 0,9545 |
| 1,7 | 0,9554 | 0,9564 | 0,9573 | 0,9582 | 0,9591 | 0,9599 | 0,9608 | 0,9616 | 0,9625 | 0,9633 |
| 1,8 | 0,9641 | 0,9649 | 0,9656 | 0,9664 | 0,9671 | 0,9678 | 0,9686 | 0,9693 | 0,9699 | 0,9706 |
| 1,9 | 0,9713 | 0,9719 | 0,9726 | 0,9732 | 0,9738 | 0,9744 | 0,9750 | 0,9756 | 0,9761 | 0,9767 |
| 2,0 | 0,9772 | 0,9778 | 0,9783 | 0,9788 | 0,9793 | 0,9798 | 0,9803 | 0,9808 | 0,9812 | 0,9817 |
| 2,1 | 0,9821 | 0,9826 | 0,9830 | 0,9834 | 0,9838 | 0,9842 | 0,9846 | 0,9850 | 0,9854 | 0,9857 |
| 2,2 | 0,9861 | 0,9864 | 0,9868 | 0,9871 | 0,9875 | 0,9878 | 0,9881 | 0,9884 | 0,9887 | 0,9890 |
| 2,3 | 0,9893 | 0,9896 | 0,9898 | 0,9901 | 0,9904 | 0,9906 | 0,9909 | 0,9911 | 0,9913 | 0,9916 |
| 2,4 | 0,9918 | 0,9920 | 0,9922 | 0,9925 | 0,9927 | 0,9929 | 0,9931 | 0,9932 | 0,9934 | 0,9936 |
| 2,5 | 0,9938 | 0,9940 | 0,9941 | 0,9943 | 0,9945 | 0,9946 | 0,9948 | 0,9949 | 0,9951 | 0,9952 |
| 2,6 | 0,9953 | 0,9955 | 0,9956 | 0,9957 | 0,9959 | 0,9960 | 0,9961 | 0,9962 | 0,9963 | 0,9964 |
| 2,7 | 0,9965 | 0,9966 | 0,9967 | 0,9968 | 0,9969 | 0,9970 | 0,9971 | 0,9972 | 0,9973 | 0,9974 |
| 2,8 | 0,9974 | 0,9975 | 0,9976 | 0,9977 | 0,9977 | 0,9978 | 0,9979 | 0,9979 | 0,9980 | 0,9981 |
| 2,9 | 0,9981 | 0,9982 | 0,9982 | 0,9983 | 0,9984 | 0,9984 | 0,9985 | 0,9985 | 0,9986 | 0,9986 |

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hi!
Was mache ich wenn ich die approximative Wahrscheinlichkeit (z.B. Wie hoch ist die Wahrscheinlichkeit das mindestens 270 von 300 eine Erkrankung haben) und ein Wert wie 14 herauskommt. Den kann ich nicht in der Tabelle ablesen…
Viele Grüße
Anton
Bei Zahlen die so groß sind dass man sie in der Tabelle nicht mehr findet, kann man als Wahrscheinlichkeit „fast 1“ nehmen, das ist dann im Bereich 0.9999….
Vorher muss aber 270 – 300 in z-Werte tranzformiert werden, dann erst weiß man welche Wahrscheinlichkeit zugehörig sein sollte.
Hey!
Wie berechne ich den Wert „Φ“ mit dem Tacshenrechner?
Ich besitze den casio fx-991DEX und ich kann zwar über den Programmpunkt „Verteilungsfunktion“ -> „Kumulierte Normal-Verteilung“ z.B. Prozentzahlen berechnen, wenn ich den Erwartungswert, die Standardabweichung und das jeweilige Intervall gegeben habe, allerdings weiß ich nicht ob und wenn ja, wie ich ganz einfach die Werte für Φ berechnen kann.
Wäre dir über eine kurze Antwort sehr sehr dankbar!
Lieben Gruß,
Simon
Den Wert für Phi müsstest du bekommen, wenn du als untere Intervallgrenze \(-\infty\) angibst, für Erwartungswert 0 und für Standardabweichung 1.
Danke für die schnelle Antwort, bin nicht der Erste, der dir das sagt, aber deine Seite ist sau gut^^
Hab mir noch zusätzlich dein Bundle gegönnt aufgrund einer bevorstehenden Klausur, hoffe, damit wenigstens einen Bruchteil zurückgeben zu können :p.
Gruß