Einführende Artikel
Zum Einstieg in das Thema Hypothesentests sollte man sich zu Beginn die folgenden beiden Artikel durchlesen:
In ihnen beschreibe ich ganz allgemein die Schritte, mit denen man einen Hypothesentest durchführt. Dadurch werden die einzelnen Teile in diesem Artikel verständlicher.
Außerdem macht es Sinn, den Artikel zum Binomialtest zu lesen, da ich dort noch etwas ausführlicher beschrieben habe, wie man die allgemeinen Prinzipien auf einen speziellen Test anwendet. Falls hier etwas nur kurz beschrieben wird, dann ist es im Artikel zum BInomialtest evtl. ausführlicher verständlicher erklärt worden.
Der Zweistichproben-t-Test
Der einfachste Fall eines t-Tests ist der Einstichproben-t-Test, den wir in einem eigenen Artikel bereits behandelt haben. Allerdings ist es in der Praxis üblicher, dass man nicht nur eine, sondern zwei Gruppen hat, und deren Mittelwerte vergleichen möchte. Ein typisches Beispiel sind Messungen, die an Patienten mit einer bestimmten Krankheit vorgenommen werden, und dann „zur Kontrolle“ an einer anderen Gruppe von gesunden Menschen.
In diesem Fall handelt es sich um zwei unabhängige Gruppen. Unabhängig bedeutet hier, dass die Personen (oder Objekte) aus der ersten Gruppe nichts mit denen aus der zweiten Gruppe zu tun haben. Im gepaarten t-Test war das anders, da waren in der ersten und zweiten Gruppe dieselben Personen, nur eben vor bzw. nach einer bestimmten Behandlung.
1. Hypothesen aufstellen
Beim t-Test gibt es, genau wie beim Binomialtest, drei verschiedene Möglichkeiten, seine Hypothesen zu formulieren. Welche Variante man verwenden muss, hängt von der Fragestellung ab, die man untersucht. Dazu drei Beispiele:
- Ein Forschungsinstitut hat in den 1960er-Jahren untersucht, ob Nichtraucher eine längere Lebenserwartung haben. Dazu wurden in einer ersten Stichprobe von 8 bereits verstorbenen Rauchern das Alter zum Todeszeitpunkt notiert, und in einer zweiten Stichprobe von 6 Nichtrauchern ebenso.
Um nachzuweisen, dass Nichtraucher eine längere Lebenserwartung haben, kommt dieser Fall in die Alternativhypothese (warum, wird hier erklärt). Wenn wir also die Lebenserwartung von Nichtrauchern mit \(\mu_N\) bezeichnen, und die der Raucher mit \(\mu_R\), lauten unsere Hypothesen:- \(H_0: \mu_N \leq \mu_R\)
- \(H_1: \mu_N > \mu_R\)
- Um nachzuweisen, dass regelmäßiges Meditieren den Blutdruck senkt, hat ein Studio bei 7 seiner meditierenden Mitglieder den Blutdruck gemessen. Als Kontrollgruppe wurden 7 zufällige Leute auf der Straße, die nicht meditieren, angehalten, und bei ihnen ebefalls der Blutdruck gemessen.
Da das Studio nachweisen möchte, dass die Meditierer einen niedrigeren durchschnittlichen Blutdruck haben, kommt dieser Fall in die Alternativhypothese. Wir bezeichnen mit \(\mu_M\) den mittleren Blutdruck von Meditierern, und mit \(\mu_N\) den der Nicht-meditierenden, und formen die folgenden Hypothesen:- \(H_0: \mu_M \geq \mu_N\)
- \(H_1: \mu_M < \mu_N\)
Es ist wohl hilfreich, wenn man diesen Fall genau betrachtet, und mit dem Beispiel aus dem Artikel zum gepaarten t-Test vergleicht: Dort wurde nämlich genau dieselbe Forschungsfrage untersucht, aber mit einem anderen Versuchsplan. Genauer gesagt: Es wurde hier kein vorher/nachher-Vergleich gemacht, in dem der Blutdruck für dieselbe Person vor und nach einer Meditation gemessen wurde, sondern es wurden zwei unabhängige Gruppen untersucht. Diese Tatsache führt dazu, dass wir in diesem Beispiel einen Zweistichproben-t-Test brauchen.
- Ein Forscher vermutet, dass ein Masterabschluss an einer Fachhochschule (FH) eher praktische Fähigkeiten vermittelt, und einer an der Universität eher theoretische Fähigkeiten. Er möchte nun untersuchen, ob diese unterschiedlichen Ansätze eine Auswirkung auf das spätere Einkommen haben. Dazu sucht er sich eine Gruppe von 100 Berufstätigen im ungefähr gleichen Alter von 40-45 Jahren, und notiert jeweils den Studienabschluss (also „Uni“ oder „FH“) sowie das Einkommen dieser Person.
Da man theoretisch beide Möglichkeiten (FH-Absolventen verdienen mehr, oder Uni-Absolventen verdienen mehr) für denkbar hält, möchte man bezüglich der Richtung unvoreingenommen vorgehen – man führt also einen zweiseitigen Test durch. Wir bezeichnen das mittlere Einkommen von FH-Absolventen mit \(\mu_F\), das der Uni-Absolventen mit \(\mu_U\). Die Hypothesen lauten dann:- \(H_0: \mu_F = \mu_U\)
- \(H_1: \mu_F \neq \mu_U\)
Die drei verschiedenen Möglichkeiten hängen also davon ab, in welche Richtung die Alternativhypothese geht (kleiner oder größer), bzw. ob sie einseitig oder – wie im dritten Beispiel – zweiseitig ist.
Für den restlichen Artikel konzentrieren wir uns auf das erste Beispiel, das mit der höheren Lebenserwartung von Nichtrauchern.
2. Test wählen
Um die Abfolge der 8 Schritte nicht zu verändern, die wir in den beiden einführenden Artikeln aufgestellt haben (erster und zweiter Artikel), nehme ich hier den 2. Schritt auch mit auf. Es ist natürlich schon klar, dass wir einen Zweistichproben-t-Test verwenden werden.
3. Signifikanzniveau festlegen
Wie in den vorherigen Artikeln schon beschrieben, legt das Signifikanzniveau die Wahrscheinlichkeit fest, mit der man einen bestimmten Fehler macht, nämlich die fälschliche Entscheidung dass die Alternativhypothese gilt, obwohl in Wirklichkeit die Nullhypothese wahr ist.
Allgemeiner Konsens ist hier ein Wert von 5%, also \(\alpha=0.05\). In besonders kritischen Fragestellungen, z.B. solchen, die die menschliche Gesundheit betreffen, muß das Signifikanzniveau oft niedriger gewählt werden, der Test wird dann konservativer. Hier wählt man z.B. \(\alpha=0.01\).
Für unsere Beispielaufgabe nehmen wir das übliche Signifikanzniveau von \(\alpha=0.05\).
4. Daten sammeln
In einer Klausur sind die Daten meist schon gegeben, aber in einer echten Untersuchung müssen wir sie natürlich erst sammeln. Beim Zweistichproben-t-Test brauchen wir, wie der Name schon sagt, zwei Stichproben. Das erreichte Lebensalter der 6 Nichtraucher sind in unserer Aufgabe die folgenden Werte:
\[ N = (80, 92, 74, 99, 69, 78) \]
Wir haben auch das Alter von 8 Rauchern erhalten:
\[ R = (81, 72, 68, 71, 59, 91, 71, 70) \]
5. Prüfgröße berechnen
Beim Zweistichproben-t-Test gibt es einige Spezialfälle, je nachdem ob die Varianz in den beiden Gruppen gleich bzw. verschieden ist, oder ob sie bekannt bzw. unbekannt ist. Ich möchte aber nicht auf alle diese Fälle eingehen, sondern nur auf den in der Praxis relevantesten: Die Varianzen der Merkmale in den zwei Gruppen sind nicht notwendigerweise gleich, und sie sind unbekannt.
Erstens tritt dieser Fall am häufigsten auf, und zweitens kann man diese Variante bei realistischen Stichproben immer, in jedem Fall, anwenden (als Faustregel gilt, wenn in beiden Gruppen mindestens 30 Beobachtungen gemacht wurden).
In diesem Fall müssen wir die folgenden Werte berechnen:
- \(\bar{x}\), der Mittelwert in der ersten Gruppe (Nichtraucher). Bei uns ist \(\bar{x} = 82\).
Vorsicht: Hier muss man aufpassen, die beiden Gruppen nicht zu verwechseln. Die Gruppe, die in den beiden Hypothesen zuerst, d.h. auf der linken Seite steht (die Nichtraucher), ist jetzt auch die erste Gruppe \(X\). Im Idealfall nennt man die Gruppen einfach von Anfang an \(X\) und \(Y\), aber es ist vielleicht zu Beginn etwas einleuchtender wenn man die Anfangsbuchstaben der zwei Gruppen verwendet. - \(n_x\), die Anzahl der Beobachtungen in der ersten Gruppe. Bei uns ist \(n_x = 6\), da wir 6 Nichtraucher untersucht haben.
- \(s^2_x\), die Varianz in der ersten Gruppe. Bei uns ist \(s^2_x = 128.4\).
- \(\bar{y}\), der Mittelwert in der zweiten Gruppe (Raucher). Bei uns ist \(\bar{y} = 72.875\). Das mittlere Lebensalter von Nichtrauchern ist also schonmal höher als das der Raucher. Ob es statistisch signifikant höher ist, finden wir jetzt heraus.
- \(n_y\), die Anzahl der Beobachtungen in der zweiten Gruppe. Bei uns ist \(n_y = 8\)
- \(s^2_y\), die Varianz in der zweiten Gruppe. Bei uns ist \(s^2_y = 89.554\).
Dann lautet die Prüfgröße \(T\):
\[ T = \frac{\bar{x} – \bar{y}}{\sqrt{\frac{s^2_x}{n_x} + \frac{s^2_y}{n_y}}} \]
Bei uns setzen wir also ein und erhalten:
\[ T = \frac{82 – 72.875}{\sqrt{\frac{128.4}{6} + \frac{89.554}{8}}} = 1.598 \]
Unsere Prüfgröße T hat also den Wert 1.598.
6. Verteilung der Prüfgröße bestimmen
Falls die Nullhypothese gilt, ist die Prüfgröße t-verteilt mit \(n_x + n_y – 2\) Freiheitsgraden:
\[ T \sim t(n_x + n_y – 2) \]
Bei uns ist das also eine t-Verteilung mit 6+8-2, also 12 Freiheitsgraden:
\[ T \sim t(12) \]
Notiz am Rande: In unterschiedlicher Literatur gibt es sowohl für den Nenner bei der Prüfgröße, als auch für die Anzahl der Freiheitsgrade hier, verschiedene Formeln. Das Thema ist etwas komplexer, aber in der Praxis vereinfacht sich das ungemein, da wir dann für die beiden Gruppen genügend Beobachtungen haben, und einen einfacheren Test verwenden können (wer es genau wissen will: Dann greift der zentrale Grenzwertsatz und wir können als Approximation die Normalverteilung statt der t-Verteilung verwenden).
In Klausuren ist es allerdings nicht machbar, Mittelwerte und Varianzen von mehr als 30 Beobachtungen zu berechnen, weswegen es in diesen Fällen dann doch immer zu diesen Formeln führt. Falls sich Formeln in euren Vorlesungen oder Formelsammlungen von den hier genannten unterscheiden, verwendet natürlich immer die Formeln die euer Professor euch vorgegeben hat.
Das grundlegende Prinzip wird sich dadurch nicht ändern, dieser Artikel ist also trotzdem sinnvoll. Nur die Zahl im Ergebnis wird ein wenig anders sein.
7. Kritischen Bereich (oder p-Wert) berechnen
Den kritischen Bereich berechnen wir genau so wie wir es beim Einstichproben-t-Test und beim gepaarten t-Test schon gemacht haben. Eine Einführung in diese Aufgabe, und ein paar weiter verdeutlichende Beispiele gibt es in diesen beiden Artikeln.
In dieser Aufgabe führen wir einen einseitigen t-Test durch, in dem die Alternative nach rechts zielt. Der kritische Bereich ist also der „höchste“ Bereich, d.h. die höchsten 5%, in die die t-Verteilung mit 12 Freiheitsgraden fällt. Mathematisch gesagt suchen wir als Schranke zu diesem Bereich das 95%-Quantil der t-Verteilung mit 12 Freiheitsgraden.
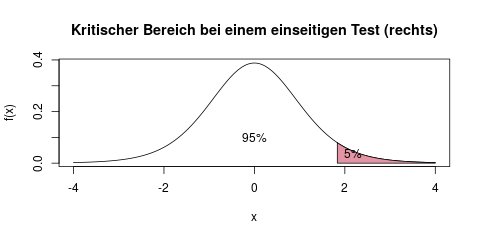 Alle Werte, die „rechts“ von dieser Schranke liegen, d.h. größer als diese Schranke sind, liegen nun im kritischen Bereich. Falls unsere Prüfgröße dort gelandet ist, lehnen wir die Nullhypothese ab.
Alle Werte, die „rechts“ von dieser Schranke liegen, d.h. größer als diese Schranke sind, liegen nun im kritischen Bereich. Falls unsere Prüfgröße dort gelandet ist, lehnen wir die Nullhypothese ab.
Die genauen Werte erhalten wir aus der Tabelle der t-Verteilung (im Artikel zur t-Verteilung ist auch genauer erklärt, wie man das macht). Die rechte Schranke ist, wie schon gesagt, das 95%-Quantil der t-Verteilung mit 12 Freiheitsgraden, und aus der Tabelle lesen wir dafür den Wert 1.782 ab. Prüfe das am besten selbst nach, es ist für eine Klausur unerlässlich, das schnell und sicher zu können.
8. Testentscheidung treffen
Für die Entscheidung haben wir jetzt alle Informationen zusammen:
- Die Prüfgröße ist \(T = 1,.598\).
- Die Schranke zum kritischen Bereich ist bei 1.782. Der kritische Bereich sind alle Werte größer als diese Schranke (da wir einen einseitigen Test rechnen, bei dem die Alternativhypothese nach rechts zielt).
Unsere Prüfgröße liegt also nicht im kritischen Bereich. Daher können wir schlussfolgern, dass wir in dieser Analyse die Nullhypothese nicht ablehnen können. Es wurde also hier kein Beweis dafür gefunden, dass Nichtraucher länger leben als Raucher.
Hinweis: Das bedeutet ausdrücklich nicht, dass wir bewiesen haben dass Nichtraucher nicht länger leben als Raucher. Denn wir können \(H_0\) niemals „statistisch beweisen“, sondern nur \(H_1\). Diese Tatsache ist in diesem Artikel genauer erklärt.
Änderungen bei den zwei anderen Beispielen
Für die übrigen zwei Beispiele aus dem 1. Schritt, wenn die Alternativhypothese entweder zweiseitig ist, oder nach links statt nach rechts zielt, verändert sich nur der kritische Bereich in Schritt 7; die Prüfgröße \(T\) wird aber auf dieselbe Weise berechnet. Die Änderungen sind identisch wie im Einstichproben-t-Test, weswegen der Abschnitt im dortigen Artikel hier genauso angewendet werden kann.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hallo,
Mir sind auch zwei kleine Fehler aufgefallen.
Unter 2. Test wählen steht: „dass wir einen Einstichproben-t-Test verwenden werden.“, womit natürlich Zweistichproben-t-Test gemeint ist.
Bei der Klausuraufgabe ist als Freiheitsgrad 14 angegeben, aber es sollte doch 13 sein oder nicht?
nx+ny–2 = 7+8-2 = 13
Mit freundlichen Grüßen
Esra
Hi nochmal – und vielen Dank! Ich habs bereits korrigiert 🙂
Viele Grüße
Alex
Hallo noch einmal,
mir ist noch ein Fehler aufgefallen, durch den es zu Verwirrung kommt: Sowohl xquer als auch yquer werden als die Gruppe „Nichtraucher“ bezeichnet. Eigentlich müsste es heißen: „𝑦¯, der Mittelwert in der zweiten Gruppe (Raucher). Bei uns ist 𝑦¯=72.875.“
Zudem verstehe ich nicht, wieso du nicht mit der Standardabweichung sondern mit der Varianz arbeitest. Die Standardabweichung macht das Einsetzen in die Formel doch viel einfacher.
Ich freue mich über deine Antwort.
Viele Grüße
Marie
Hi Marie,
das mit den Nichtrauchern war ein Tippfehler, den habe ich gerade korrigiert – vielen Dank!
Bei der Varianz hast du durch \(n\) geteilt, aber musst stattdessen durch \(n-1\) teilen. Hier ist das nochmal erklärt:
https://www.crashkurs-statistik.de/streuungsparameter-spannweite-quartilsabstand-varianz-standardabweichung/#varianz
Viele Grüße
Alex
Viele Grüße
Alex
Hallihallo,
zunächst einmal vielen Dank für die tollen Erklärungen und die verständlichen Beispiele. Deine Website rettet mir derzeit meine Statistikklausur.
Beim Durchrechnen deines Raucherbeispiels komme ich auf eine Varianz von 78,359375 (gerundet 78,36) für die Raucher und eine Varianz von 107 für die Nichtraucher. Ich habe gerechnet (xi1-x(quer)zum quadrat+(xi2-xquer) zum quadrat usw. Am Ende habe ich das Ergebnis durch die Anzahl der Beobachtungen geteilt. Bei den Rauchern durch 8 und bei den Nichtrauchern durch 6.
Bei der Varianz Ich habe es zwei mal durchgerechnet und ich wüsste nicht wo ich einen Fehler gemacht haben soll.
Es wäre super, wenn du das Ergebnis vielleicht noch einmal überprüfen würdest.
Liebe Grüße
Marie