Was ist ein Chi-Quadrat-Test?
Den Chi-Quadrat-Test gibt es eigentlich nicht. Genauso wie es einige verschiedene t-Tests gibt, so bezeichnet man mit „Chi-Quadrat-Test“ (bzw. \(\chi^2\)-Test, das ist der griechische Buchstabe „Chi“) auch eine Reihe von verschiedenen Tests. Was sie alle gemeinsam haben, ist dass ihre Prüfgröße eine Chi-Quadrat-Verteilung hat.
Ein häufiger Anwendungsfall für den Chi-Quadrat-Test, den wir auch in diesem Artikel behandeln, ist das Testen ob zwei nominale Variablen voneinander abhängig sind, ob sie sich also gegenseitig beeinflussen. Wir fragen z.B. 80 Personen nach ihrem Geschlecht, und nach der von ihr zuletzt gewählten Partei. Wenn wir nun untersuchen möchten ob Frauen und Männer ein unterschiedliches Wahlverhalten haben, geht das mit dem Chi-Quadrat-Test.
Allgemein formuliert testen wir, ob zwei nominalskalierte Variablen abhängig sind. Falls z.B. das Geschlecht einer Person und die zuletzt gewählte Partei voneinander abhängig sind, und wir die gewählte Partei erraten wollen, dann hilft es uns, von einer bestimmten Person das Geschlecht zu kennen. Bei unabhängigen Variablen würde uns die eine Variable nicht helfen, die andere vorherzusagen. Ein Beispiel für zwei unabhängige Variablen wäre das Geschlecht einer Person, und ihre Augenfarbe. Es hilft uns wahrscheinlich nicht dabei, die Augenfarbe von Person X vorherzusagen, wenn wir erfahren, dass es sich dabei um eine Frau handelt.
Eine weitere Analyse die einen Chi-Quadrat-Test verwendet, wäre das Testen ob eine einzelne nominale Variable eine bestimmte Verteilung hat. So könnte z.B. ein Betreiber des öffentlichen Nahverkehrs vermuten, dass bei ihm 30% der Passagiere eine Einzelfahrkarte haben, 65% eine Monatskarte, und 5% Schwarzfahrer sind. Wenn es nun 100 Personen nach ihrer Fahrkarte fragt, kann es mit diesen Daten einen Chi-Quadrat-Test durchführen, um seine Annahme zu überprüfen. Diese Variante wird oft auch Chi-Quadrat-Anpassungstest genannt (Dieser Fall findet sich auch in der Tabelle zur Testwahl wieder, wird aber hier nicht behandelt).
Einführende Artikel
Zum Einstieg sollte man sich zu Beginn die folgenden beiden Artikel durchlesen:
In ihnen beschreibe ich ganz allgemein die Schritte, mit denen man einen Hypothesentest durchführt. Dadurch werden die einzelnen Teile in diesem Artikel verständlicher.
1. Hypothesen aufstellen
Wir betrachten in diesem Artikel das oben erwähnte Beispiel. Wir fragen 80 Personen nach ihrem Geschlecht, und der zuletzt gewählten Partei. Die Hypothesen bei diesem Test lauten immer gleich:
- \(H_0\): Die beiden Variablen \(X\) und \(Y\) sind unabhängig
- \(H_1\): Die beiden Variablen \(X\) und \(Y\) sind voneinander abhängig
Welche der Variablen man \(X\) und welche man \(Y\) nennt, ist eigentlich egal. Man kann auch andere Buchstaben verwenden die man sich leichter merken kann, z.B. \(G\) für das Geschlecht, und \(P\) für die Partei.
Welche Hypothese die Null- und welche die Alternativhypothese wird, ist bei dieser Aufgabenformulierung manchmal nicht eindeutig formuliert. Aber man kann sich merken, dass man solche Tests immer nur in eine Richtung rechnen kann: Die Situation „die beiden Variablen sind abhängig“ muss immer in die Alternativhypothese.
2. Test wählen
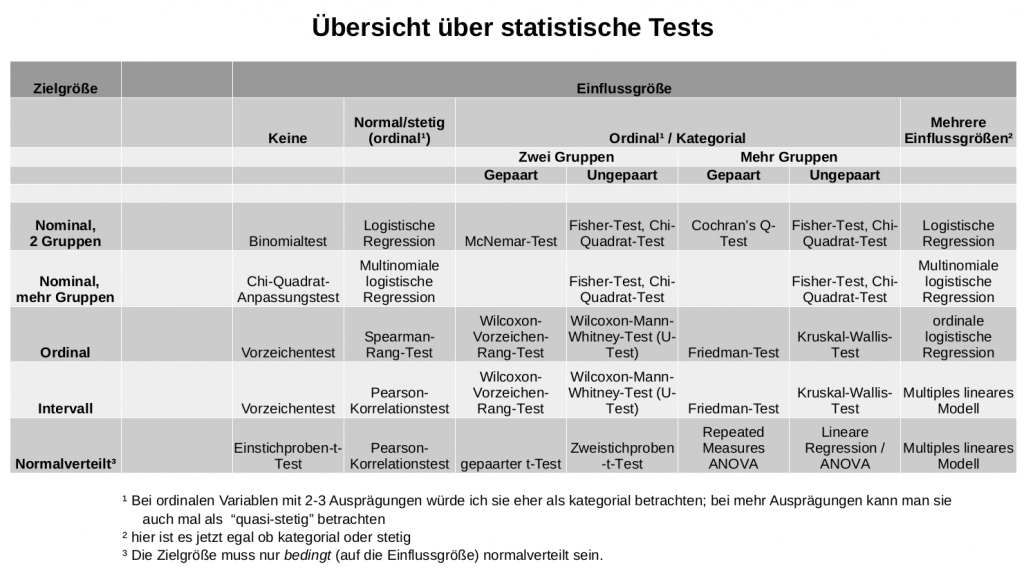
Wir führen hier einen Chi-Quadrat-Test durch. Die Tabelle zur Testwahl hätte uns das auch vorgeschlagen, da wir eine nominale Zielgröße haben (die Partei) und eine nominale Einflussgröße (das Geschlecht).
Notiz am Rande: Der Fisher-Test, der in dieser Tabelle als Alternative vorgeschlagen wird, hat das gleiche Ziel wie der Chi-Quadrat-Test, aber ist im Ergebnis etwas genauer – dafür aber auch rechenaufwändiger. Als Faustregel hat sich eingebürgert, dass man den Chi-Quadrat-Test immer dann verwenden darf, wenn in jeder einzelnen Zelle der in Schritt 4 erstellten Kreuztabelle eine Zahl größer oder gleich 5 steht.
3. Signifikanzniveau festlegen
Wie in allen anderen besprochenen Tests hier können wir auch beim Chi-Quadrat-Test das Signifikanzniveau wählen. Hier verwenden wir die üblichen 5%, also setzen wir das Signifikanzniveau \(\alpha = 0.05\) fest.
4. Daten sammeln
Die Ausgangslage, die wir für einen Chi-Quadrat-Test benötigen, ist immer eine Kreuztabelle der beiden Variablen.
Die Ergebnisse bekommen wir als Liste, aber wir können sie einfach in eine Kreuztabelle zusammenfassen. Als Ausgangssituation haben wir oft eine Liste der folgenden Form:
| Person \(i\) | Geschlecht | Partei |
|---|---|---|
| 1 | männlich | CDU/CSU |
| 2 | weiblich | Sonstige |
| 3 | männlich | SPD |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
Wir formen diese Daten um in eine Kreuztabelle (Diese Tabelle haben wir im Artikel zu Kreuztabellen schon mal gesehen):
| SPD | CDU/CSU | FDP | Grüne | Sonstige | Summe | |
|---|---|---|---|---|---|---|
| Männer | 26 | 22 | 8 | 12 | 16 | 84 |
| Frauen | 36 | 28 | 14 | 14 | 24 | 116 |
| Summe | 62 | 50 | 22 | 26 | 40 | 200 |
5. Prüfgröße berechnen
Die Prüfgröße kennen wir bereits aus der deskriptiven Statistik. Sie ist nämlich exakt dasselbe wie der Chi-Quadrat-Koeffizient \(\chi^2\). Die Berechnung dieses Wertes ist im dortigen Artikel erklärt, auch die Herleitung, warum man ihn so berechnet, wird dort erläutert. Ich gebe hier daher die Herleitung der Prüfgröße relativ knapp erklärt wieder.
Wir gehen in zwei Schritten vor. Zuerst berechnen wir die Unabhängigkeitstabelle, und danach den Chi-Quadrat-Koeffizienten, d.h. die Prüfgröße.
Um die Unabhängigkeitstabelle zu erstellen, beginnen wir mit der (bis auf die Randhäufigkeiten) leeren Kreuztabelle der Umfragewerte:
| SPD | CDU/CSU | FDP | Grüne | Sonstige | Summe | |
|---|---|---|---|---|---|---|
| Männer | 84 | |||||
| Frauen | 116 | |||||
| Summe | 62 | 50 | 22 | 26 | 40 | 200 |
Dort fügen wir jetzt für jede Zelle die erwartete Häufigkeit ein, d.h. die Anzahl an Personen, die wir erwarten würden wenn die beiden Merkmale „Geschlecht“ und „Partei“ nichts miteinander zu tun hätten. Die Formel dafür (für Zeile \(i\) und Spalte \(j\)) lautet:
\[ e_{ij} = \frac{h_{i\cdot} \cdot h_{\cdot j}}{n} \]
Zum Beispiel ist der erwartete Anteil der männlichen FDP-Wähler \(e_{13} = \frac{84\cdot 22}{200} = 9.24\).
Wie gesagt, im Artikel zum Chi-Quadrat-Koeffizienten ist dieses Vorgehen ein bisschen detaillierter erklärt.
Die erwarteten Häufigkeiten können wir jetzt in die Tabelle eintragen, um den zweiten Schritt, das Berechnen von \(\chi^2\), übersichtlicher machen zu können:
| SPD | CDU/CSU | FDP | Grüne | Sonstige | Summe | |
|---|---|---|---|---|---|---|
| Männer | 26.04 | 21 | 9.24 | 10.92 | 16.80 | 84 |
| Frauen | 35.96 | 29 | 12.76 | 15.08 | 23.20 | 116 |
| Summe | 62 | 50 | 22 | 26 | 40 | 200 |
Mit den übersichtlich gesammelten Werten für \(e_{ij}\) können wir nun die Prüfgröße anhand der folgenden Formel berechnen:
\[ \chi^2 = \sum_{i=1}^I \sum_{j=1}^J \frac{(h_{ij}-e_{ij})^2}{e_{ij}} \]
Was das in Worten bedeutet: Wir müssen für jede der 10 Zellen den Unterschied zwischen tatsächlicher und erwarteter Häufigkeit berechnen, diesen Unterschied dann quadrieren, und ihn nochmal durch die erwartete Häufigkeit teilen. Die so erhaltenen 10 Werte summieren wir einfach auf, und das Ergebnis ist die Prüfgröße.
Für die Zelle „weibliche FDP-Wähler“, also Zeile 2 und Spalte 3, sähe das beispielhaft so aus: \(\frac{(14-12.76)^2}{12.76} = 0.1205\)
Alle 10 Werte, wer es selbst nachrechnen möchte, fasse ich hier kurz zusammen:
| SPD | CDU/CSU | FDP | Grüne | Sonstige | |
|---|---|---|---|---|---|
| Männer | 0.00006 | 0.0476 | 0.1664 | 0.1068 | 0.0381 |
| Frauen | 0.00004 | 0.0344 | 0.1205 | 0.0773 | 0.0276 |
Und die fertige Prüfgröße \(\chi^2\) ist jetzt einfach die Summe dieser 10 Werte:
\[ \chi^2 = 0.6188 \]
6. Verteilung der Prüfgröße bestimmen
Die Prüfgröße heißt \(\chi^2\), und sie hat passenderweise auch eine \(\chi^2\)-Verteilung. Wir müssen zum richtigen Ablesen der kritischen Werte allerdings noch die Anzahl der Freiheitsgrade bestimmen. Was damit gemeint ist, ist für einführende Statistikveranstaltungen nicht so wichtig – man darf nur nicht vergessen, diesen Wert zu berechnen, und dann in der Verteilungstabelle auch am richtigen Ort nachzusehen.
Die Prüfgröße ist also \(\chi^2\)-verteilt, und zwar mit \((I-1)\cdot (J-1)\) Freiheitsgraden. Dabei ist mit \(I\) die Anzahl der Zeilen in der Kreuztabelle gemeint, und mit \(J\) die Anzahl der Spalten.
Bei unserem Beispiel sind es also \((2-1) \cdot (5-1) = 4\) Freiheitsgrade.
7. Kritischen Bereich (oder p-Wert) berechnen
Beim Chi-Quadrat-Test gibt es glücklicherweise nur eine Testvariante. Beim t-Test hatten wir dagegen drei mögliche Testrichtungen, je nachdem wie die Alternativhypothese formuliert war: kleiner, größer, oder ungleich einem vorher bestimmten Mittelwert.
Das Berechnen des kritischen Bereichs ist beim Chi-Quadrat-Test also im Gegensatz zum t-Test sehr einfach: Wenn unser Signifikanzniveau \(\alpha\) die üblichen 5% sind, also \(\alpha=0.05\), dann suchen wir das 95%-Quantil (also allgemein \(1-\alpha\)) der \(\chi^2\)-Verteilung mit den vorher berechneten Freiheitsgraden – bei uns 4.
In der Verteilungstabelle lesen wir dann ab: Für 4 Freiheitsgrade und dem Quantil 0.95, also 95%, beträgt der Wert 9.488.
Die Schranke zum kritischen Wert ist also 9.488, und beim Chi-Quadrat-Test ist der kritische Bereich immer der Bereich über der kritischen Schranke. Das heißt, dass alle Prüfgrößen über 9.488 in unserem Fall dazu führen dass wir die Nullhypothese ablehnen, und damit die beiden Variablen „Geschlecht“ und „Partei“ voneinander abhängig sind.
8. Testentscheidung treffen
Im 5. Schritt haben wir die Prüfgröße berechnet als 0.6188. Der kritische Bereich, den wir im 7. Schritt berechnet haben, ist der Bereich über 9.488. Da unsere Prüfgröße aber nicht im kritischen Bereich liegt, können wir in dieser Analyse die Nullhypothese nicht ablehnen.
Wir konnten also hier keine ausreichenden Beweise dafür finden, dass das Wahlverhalten von Männern und Frauen unterschiedlich ist.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!