Mit der Spearman-Korrelation misst man ebenso wie mit der Pearson-Korrelation den Zusammenhang zwischen zwei Variablen. Er nimmt ebenso Werte von -1 (perfekte negative Korrelation) bis +1 (perfekte positive Korrelation) an, und ist nahe bei 0, falls gar keine Korrelation vorliegt.
Der Spearman-Korrelationskoeffizient \(r_\text{Sp}\) wird auch Rangkorrelationskoeffizient genannt, weil nur er einen kleinen, aber entscheidenden Unterschied zum klassischen Pearson-Korrelationskoeffizienten \(r\) hat:
Die Korrelation wird nicht zwischen den Datenpunkten selbst, sondern zwischen ihren Rängen berechnet. Ein Beispiel veranschaulicht das schnell:
Beispiel: Alter vs. Performance beim 100m-Lauf
Wir möchten den Zusammenhang zwischen dem Alter einer Person und ihrer Performance beim 100-Meter-Sprint analysieren. Dazu messen wir von 6 Personen das Alter in Jahren, und die Zeit für 100 Meter in Sekunden:
| Person \(i\) | Alter \(x_i\) | Zeit in Sekunden \(y_i\) |
|---|---|---|
| A | 59 | 14.61 |
| B | 35 | 11.80 |
| C | 43 | 14.34 |
| D | 23 | 13.03 |
| E | 42 | 14.18 |
| F | 27 | 11.02 |
Wir können nun die klassische Pearson-Korrelation zwischen den Variablen „Alter“ und „Zeit“ berechnen:
\[r = \frac{\sum_{i=1}^n (x_i – \bar{x}) (y_i – \bar{y})}{ \sqrt{\sum_{i=1}^n (x_i – \bar{x})^2} \cdot \sqrt{\sum_{i=1}^n (y_i – \bar{y})^2} } \]
Wer zur Übung nachrechnen will, das Ergebnis ist \(r = 0.73\). Um für dieselben Daten nun die Spearman-Korrelation zu berechnen, betrachten wir für beide Merkmale nicht die tatsächlichen Werte „Alter“ und „Zeit in Sekunden“, sondern deren Ränge. Wir arbeiten also mit den Platzierungen auf der Siegertreppe statt mit der tatsächlichen Zeit, und ebenso mit dem „Platz“ oder dem Rang des Alters.
In der Tabelle entstehen dafür zwei neue Spalten für die beiden Ränge. Die Ränge werden hier aufsteigend vergeben, was bedeutet dass die kleinste Zahl den Rang 1 erhält, usw.:
| Person \(i\) | Alter \(x_i\) | Rang des Alters \(\text{rang}(x_i)\) | Zeit in Sekunden \(y_i\) | Platzierung \(\text{rang}(y_i)\) |
|---|---|---|---|---|
| A | 59 | 6 | 14.61 | 6 |
| B | 35 | 3 | 11.80 | 2 |
| C | 43 | 5 | 14.34 | 5 |
| D | 23 | 1 | 13.03 | 3 |
| E | 42 | 4 | 14.18 | 4 |
| F | 27 | 2 | 11.02 | 1 |
Den Spearman-Korrelationskoeffizient erhält man nun, wenn man die Formel der Korrelation nicht auf die Variablen „Alter“ und „Zeit“ anwendet, sondern auf deren Ränge:
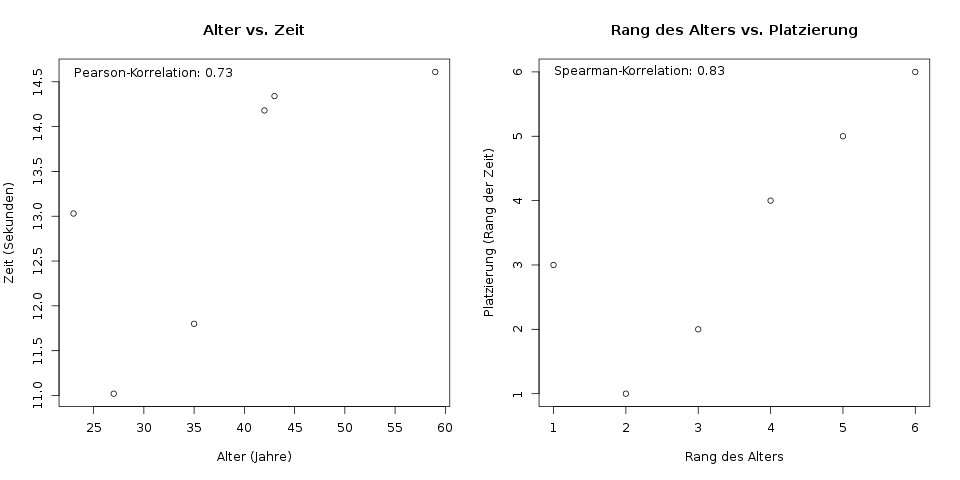
Links ist das Alter und die Zeit für 100 Meter in einem Scatterplot dargestellt. Aus diesen Daten wird die Pearson-Korrelation \(r\) berechnet. Rechts sind die dazugehörigen Ränge (jeweils von 1 bis 6) dargestellt. Mit diesen Rängen berechnet man den Spearman-Korrelationskoeffizienten \(r_\text{Sp}\).
Die Formel für die Spearman-Korrelation ist genau dieselbe wie für die Pearson-Korrelation, nur werden die Daten \(x_i\) und \(y_i\) mit ihren jeweiligen Rängen ersetzt:
\[r_\text{Sp} = \frac{\sum_{i=1}^n (\text{rang}(x_i) – \overline{\text{rang}(x)}) (\text{rang}(y_i) – \overline{\text{rang}(y)})}{ \sqrt{\sum_{i=1}^n (\text{rang}(x_i) – \overline{\text{rang}(x)})^2} \cdot \sqrt{\sum_{i=1}^n (\text{rang}(y_i) – \overline{\text{rang}(y)})^2} } \]
Es ist wichtig zu verstehen dass dieser Koeffizient genauso berechnet wird wie die Pearson-Korrelation, und der einzige Unterschied ist, dass die Ränge statt der Originaldaten verwendet werden. Die Formel und das Vorgehen sind aber genau dasselbe wie im Artikel zur Pearson-Korrelation beschrieben.
Zur Übung: Berechne nun die Spearman-Korrelation dieser Daten. Verwende dazu die Ränge \(\text{rang}(x_i)\) und \(\text{rang}(y_i)\) aus der obigen Tabelle. Für die Berechnung kannst du je nach Vorliebe Formel 1 oder Formel 2 aus dem Artikel zur Pearson-Korrelation verwenden. Der resultierende Wert soll \(r_\text{Sp} = 0.83\) ergeben.
Zur Interpretation kann man nun sagen, dass mit steigendem Rang des Alters auch der Rang des Platzes ansteigt. Vorsicht. Ein „steigender“ Rang heißt hier, dass die Zahl des Platzes höher wird, die Person also langsamer läuft und später ins Ziel kommt! Das heißt in klaren Worten: Ältere Personen werden tendenziell später im Ziel ankommen.
Eine kurze Bemerkung noch: Die Ränge könnte man auch andersrum vergeben, dass also die älteste Person (oder die langsamste Person) den Rang 1 bekommt. Dann würde sich der Spearman-Koeffizient nur im Vorzeichen ändern, aus \(r_\text{Sp} = 0.83\) würde also \(r_\text{Sp} = -0.83\) werden. Die Interpretation würde dann etwas anders ablaufen, aber zum selben Ziel kommen: Die negative Korrelation bedeutet, dass mit steigendem Rang des Alters (d.h. jüngere Personen) der Rang der Platzierung sinkt (d.h. die Person schneller im Ziel ankommt). Hier also in klaren Worten: Je jünger eine Person wird, desto schneller kommt sie im Ziel an. Und daher genau dasselbe wie vorher.
Was ist der Effekt davon, die Ränge statt der Originaldaten zu nehmen?
Da bei der Spearman-Korrelation die Ränge verwendet werden, sind dort die tatsächlichen Abstände zwischen z.B. Platz 1 und Platz 2 egal. Die Spearman-Korrelation ist immer dann 1, wenn der niedrigste Wert für \(x\) gepaart ist mit dem niedrigsten Wert von \(y\), usw.
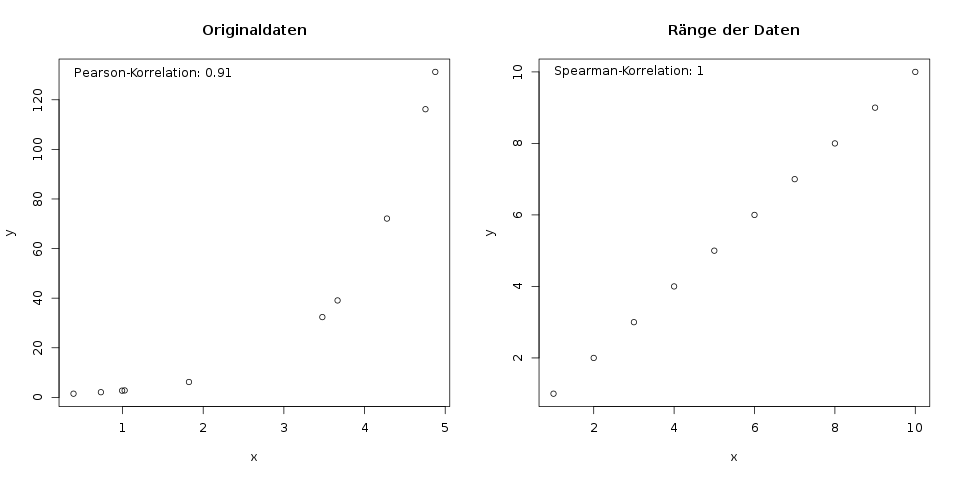
Links ist ein Scatterplot für Beispieldaten \(x\) und \(y\). Der niedrigste \(x\)-Wert gehört zum niedrigsten \(y\)-Wert, usw., jedoch ist der Zusammenhang nicht linear, sondern folgt einer Kurve. Rechts sieht man nun die Ränge der Daten gegeneinander geplottet. Der hieraus resultierende Spearman-Korrelationskoeffizient ist genau 1.
Mathematisch sagt man: Die Spearman-Korrelation misst den monotonen Zusammenhang, während die Pearson-Korrelation den linearen Zusammenhang misst.
Was passiert bei gleichen Rängen, also „Unentschieden“?
Es kann passieren, dass z.B. zwei oder mehr Werte für \(x\) denselben Wert annehmen. In diesem Fall wird den entsprechenden Werten der Durchschnittsrang zugewiesen. Hierzu drei Beispiele, hätten die Personen aus dem obigen 100-Meter-Sprint stattdessen ein anderes Alter gehabt:
| Alter \(x_i\) | 23 | 27 | 27 | 35 | 43 | 59 |
|---|---|---|---|---|---|---|
| Rang \(\text{rang}(x_i)\) | 1 | 2.5 | 2.5 | 4 | 5 | 6 |
In der obigen Tabelle haben zwei Personen dasselbe Alter, deren Ränge 2 und 3 wären. Daher bekommen beide Personen den Durchschnittsrang 2.5.
| Alter \(x_i\) | 23 | 27 | 35 | 35 | 35 | 59 |
|---|---|---|---|---|---|---|
| Rang \(\text{rang}(x_i)\) | 1 | 2 | 4 | 4 | 4 | 6 |
Hier haben drei Personen dasselbe Alter. Deren Ränge wären 3, 4, und 5. Der resultierende Durchschnittsrang für alle drei Personen ist also 4.
Eine kürzere Formel für die Spearman-Korrelation
Das oben angegebene Vorgehen zur Berechnung von \(r_\text{Sp}\) ist zwar (hoffentlich) einleuchtend und nachvollziehbar, aber die Formel ist doch sehr aufwändig auszurechnen. Es gibt zum Glück eine kürzere Formel, mit der die Spearman-Korrelation schneller ausgerechnet werden kann.
\[ r_\text{Sp} = 1 – \frac{6 \cdot \sum_{i=1}^n d_i^2}{n\cdot (n^2 -1)} \]
Vorsicht: Diese Formel darf man nur dann anwenden, wenn es keine Bindungen in den Daten gibt. Es müssen also alle \(x_i\) verschieden voneinander sein, und außerdem alle \(y_i\) voneinander verschieden sein. Andernfalls kommt mit dieser Formel ein anderes Ergebnis heraus.
Hier ist \(d_i\) die Rangdifferenz, d.h. der Unterschied zwischen den beiden Rängen für eine Beobachtung. Wenn also im oberen Beispiel jemand der jüngste ist (also sein Rang des Alters 1 ist), und das drittschnellste Ergebnis gelaufen ist (also der Rang der Platzierung 3 ist), ist die Rangdifferenz \(d_i = 1 – 3 = -2\). Diese Differenz bestimmen wir nun für jeden Läufer:
| Person \(i\) | Alter \(x_i\) | Rang des Alters \(\text{rang}(x_i)\) | Zeit in Sekunden \(y_i\) | Platzierung \(\text{rang}(y_i)\) | Rangdifferenz \(d_i = \text{rang}(x_i) – \text{rang}(y_i)\) |
|---|---|---|---|---|---|
| A | 59 | 6 | 14.61 | 6 | 0 |
| B | 35 | 3 | 11.80 | 2 | 1 |
| C | 43 | 5 | 14.34 | 5 | 0 |
| D | 23 | 1 | 13.03 | 3 | -2 |
| E | 42 | 4 | 14.18 | 4 | 0 |
| F | 27 | 2 | 11.02 | 1 | 1 |
Somit können wir die quadrierten (nicht vergessen!) Rangdiffernzen aufsummieren:
\[ \sum_{i=1}^n d_i^2 = 0^2 + 1^2 + 0^2 + (-2)^2 + 0^2 + 1^2 = 6 \]
Dieses Ergebnis setzen wir in die obige Formel nun ein:
\[ \begin{align*} r_\text{Sp} &= 1- \frac{6 \cdot \sum_{i=1}^n d_i^2}{n\cdot (n^2 -1)}\\ &= 1- \frac{6 \cdot 6}{6 \cdot (6^2 – 1)}\\ &= 0.828\end{align*} \]
Es kommt auf diesem Weg natürlich derselbe Wert für die Spearman-Korrelation heraus, \(r_\text{Sp} = 0.83\)

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hey! Danke für die tollen Erklärungen.
Eine Frage: Fehlt bei deiner Formel für Pearsons r nicht das 1/n ?
Du hast die Summe aller Produkte aus den Abständen der Ausprägungen vom Mittelwert im Zähler und das Produkt der beiden Standardabweichungen im Nenner. Der Nenner passt meines Erachtens, aber im Zähler fehlt doch das oben genannte 1/n, damit der Durchschnitt hinsichtlich der Fallzahl gegeben ist?
Lieben Gruß, Franzi
Das 1/n steht eigentlich sowohl im Zähler als auch im Nenner, und damit kürzt es sich dann raus.
VG
Alex
Hallo, ist die 6 als Vorfaktor im Zähler der vereinfachten Formel immer diese Zahl oder ist das die Anzahl der Ränge? Danke für deine verständlichen Beiträge und liebe Grüße !
Das ist eine feste 6. Anderenfalls hätte ich \(n\) hingeschrieben, um das deutlicher zu machen 🙂
Hallo,
danke für die super Erklärung!
Ich habe für meine ordinal skalierten Variablen den Rangkorrelationskoeffizient nach Spearman angewendet um die Stärke des Zusammenhangs festzustellen.
Darf ich obwohl ich kein Intervallskaliertes Merkmal habe den t-Test anwenden ? Oder welcher Test wäre auf Prüfung der Signifikanz nun der Richtige?
Vielen Dank im Voraus.
Hi,
ich habe dazu gerade vor einer Woche hier einen Artikel geschrieben:
https://www.crashkurs-statistik.de/welchen-statistischen-test-soll-ich-waehlen/
Hilft dir das weiter? Wenn nicht, sag Bescheid, wo er noch unklar ist, den muss ich bestimmt noch ein/zwei mal überarbeiten 🙂
Hallo,
danke für deine schnelle Antwort.
Ich verzweifle momentan eher daran wie ich nun ermitteln kann ob der Korrelationskoeffizient signifikant ist? Welchen Signifikanztest wende ich nach Ermittlung des Koeffizient nach Spearman an ?
Danke und viele Grüße
Ich kommen nicht auf den Wert 0,73
Bei mir kommt der Wert 0,828 als Ergebnis raus.
14,5/ Wurzel aus 17,5 ×17,5
ist die Rechnung bei mir am Ende. Ich habe die Rangfolge umgekehrt genommen d.h von 1 aufsteigend
Das passt. Die Pearson-Korrelation ist 0,73, und die Spearman-Korrelation ist 0,83 🙂
Hallo,
in einer Aufgabe muss ich ermitteln, ob zwischen den Noten zweier Fächer ein Zusammenhang besteht und dafür ein geeignetes Maß auswählen.
Die Noten sind mit Kommastellen ausgedrückt, also z.B. 1,3 oder 1,7.
Handelt es sich hier um eine Ordinal- oder Intervallskala? Und verwende ich dann die Rangkorrelation oder den Korrelationskoeffizienten? Eigentlich kann man für Noten ja einen arith. Mittelwert berechnen. Das müsste ja für eine Intervallskala sprechen.
Über einen Tipp wäre ich sehr dankbar.
VG Sophie
Hi,
dazu steht in diesem Artikel ein bisschen was:
https://www.crashkurs-statistik.de/merkmals-und-skalentypen/#skalentypen
Auch in den Kommentaren wurde diese Frage schonmal gestellt, da findest du bestimmt auch was hilfreiches 🙂
Viele Grüße,
Alex
Vielen Dank für die Super Erklärung! 🙂
Ich habe es soweit verstanden, allerdings komme ich einfach nicht bei der ersten Gleichung auf r=0.73 😀
Was genau habt ihr da für Zahlenwerte?
Ich habe bei x= 229 , y=78,98 , x quer= 38,16 und y quer=13,163
Somit ist die Gleichung doch:
(229-38,16)x(79,98-13.163)
_____________________________
Wurzel aus: (229-38,16)²x(79,98-13,163)²
oder nicht? Bei mir kommt immer 1 raus.
Danke schonmal! 🙂
Hi,
du hast die Reihenfolge vertauscht: Du darfst z.B. im Zähler nicht zuerst alle \(x_i\) aufsummieren und danach multiplizieren. Ich hab die Formel in diesem Artikel ganz ausgeschrieben:
http://www.crashkurs-statistik.de/der-korrelationskoeffizient-nach-pearson/
Dort unter der Überschrift „Formel 1“ siehst du wie man das genau ausrechnet – da musst du dann nur die Zahlen ersetzen. Ich hoffe das hilft 🙂
VG
Alex
Hallo Alex,
Vielen Dank für die leicht verständlichen Erklärungen. Anstatt 200 Seiten Skripte und Bücher zu einem Unterpunkt zu lesen, lese ich lieber Deinen Blog. Das bringt mich deutlich weiter. Überhaupt nicht verwirrend. Ich hoffe, ich bestehe damit meine Statistikklausur.
Eine Verständnisfrage hätte ich jedoch: Du schreibst, dass Spearman den monotonen Zusammenhang und Pearson den linearen Zusammenhang darstellt. Auf der Webpage der Methodenberatung heißt es, „Die Rangkorrelationsanalyse nach Spearman berechnet den linearen Zusammenhang zweier mindestens ordinalskalierter Variablen.“
Ist damit wieder was anderes gemeint? Ich bin verwirrt.
Vielen Dank
Ines
Hi,
ich glaube, das Wort „linearen“ muss aus dem Satz entfernt werden. Oder eben ersetzt durch das Wort „monotonen“. So wie es jetzt da steht, stimmt es in meinen Augen nicht.
VG,
Alex
Danke, ich halte mich an Dich 🙂
Danke für die Erklärungen.
Habe da noch eine Verständnisfrage, zu der ich bisher leider nichts in der Literatur gefunden habe.
Ich führe eine Vollerhebung durch und möchte Korrelationen zwischen Prädiktoren und Kriterien berechnen. Für die Pearson-Korrelation ist ja eine Voraussetzung die Normalverteilung.
Spielt die Normalverteilung bei einer Vollerhebung eigentlich eine Rolle oder kann ich diese vernachlässigen?
Und kann ich ohne weiteres Pearson-Korrelationskoeffizienten und Spearman-Koeffizienten miteinander vergleichen?
Vielen Dank für die Unterstützung.
Hallo,
– eine Normalverteilung ist für die Pearson-Korrelation keine Voraussetzung.
– Pearson- und Spearman kann man nicht direkt vergleichen, da sollte man immer dieselbe Variante wählen.
VG,
Alex
Hallo,
ich möchte Korrelationen zwischen Items zu verschiedenen Zeitpunkten messen. Die Wichtigkeit der Items wird auf einer Likert-Skala von 1-5 bewertet.
Ein Beispiel: Das Item „Mir hat alternative Medizin geholfen“ soll zum Zeitpunkt der Diagnose einer Krankheit und zum Zeitpunkt der Wiedereingliederung in den Beruf mit Werten von 1 bis 5 bewertet werden.
Nun möchte ich herausfinden, ob eine Korrelation zwischen den Werten besteht.
In meiner Stichprobe sind aktuell 85 Teilnehmer.
Ich würde den Rang-Korrelationskoeffizienten nach Spearman benutzen, da die Likert-Skala ja schon eher einen Rang widerspiegelt, als metrische Abstufungen – ist das richtig?
Für den Fall, dass das Programm R bekannt ist: ermittelt R die Ränge automatisch oder muss ich dem Programm noch „sagen“, wie die Ränge sind?
Vielen Dank für die Hilfe!
Viele Grüße,
Christina
Die Spearman-Korrelation bildet die Ränge automatisch. Du kannst sie also auch verwenden wenn die Originaldaten noch gar nicht in Ränge transformiert wurden.
Im Endeffekt ist die Spearman-Korrelation dasselbe wie wenn du die Pearson-Korrelation der Ränge berechnest. Für Likert-Daten sollten die Ergebnisse fast gleich sein, da ist es dann egal.
VG,
Alex
Hallo Alex,
lese ich folgedes:Die Spearman-Korrelation misst den monotonen Zusammenhang, während die Pearson-Korrelation den linearen Zusammenhang misst.
Was versteht man mathematisch unter dem monotonen Zusammenhang?
Wenn du bitte dazu ein Beispiel als mathematische Funktion bilden würdest, wäre ich dafür dankbar.
VG
Shukuhi
Hi,
die zweite Grafik im Artikel ist genau so ein monotoner Zusammenhang. Die Funktion dazu wäre \(y=\exp (x)\).
VG,
Alex
Wenn ich bspw. Daten habe mit dem Gewicht von Personen und Daten über das geschätzte Gewicht habe, nutze ich dann Pearson oder Spearman, um Messen zu können, wie gut geschätzt wurde?
Mir ist da der Unterschied nicht klar und ich erhalte bei mir derzeit eine Differenz der beiden Befehle von knapp 1% , allerdings weiß ich nicht, welche nun richtig ist.
Vielen Dank vorab
„Richtig“ und „falsch“ gibt es da nicht, das sind einfach zwei verschieden Möglichkeiten, je nachdem welche Eigenschaften man für das Korrelationsmaß haben möchte. Aber der bekanntere, die „Standardmethode“, ist die Pearson-Korrelation. Damit fährt man immer gut 🙂
Okay, vielen Dank Alex!
War mir unsicher, ob ich beim Spearman nicht etwas genauere Werte erhalte aufgrund der Möglichkeit, dass das Gewicht weniger geschätzt werden konnte und somit eine negative Abweichung entsteht. Das die Berechnung dann eine andere ist, aufgrund der positiven und negativen Differenzen.
Ich soll ganz allgemein eine Situation erklären, in der beide Koeffizienten stark voneinander abweichen würden. Da komme ich nicht weiter…
Das zweite Bild in diesem Artikel zeigt z.B. so eine Situation.
LG,
Alex
und wie lässt sich das Verallgemeinern?
Sehr schön beschrieben, Danke!
Hallo, super Erklärung. Kurze Frage, wie sortiert man Noten fängt man mit der schlechtesten Note an? Also ungenügend würde den Rang 1, mangelhaft 2 bekommen?
Danke 🙂
Die beste Note würde ich auf Rang 1 setzen. Denk dir den Rang einfach als Platzierung 🙂
Deine Seite ist echt super! Endlich mal jemand der Statistik verständnisvoll erklärt! Da kann man sich schon fast auf die Prüfung freuen 😀
Vielen Dank!
Hallo,
man könnte noch den Kendalls Tau angeben als alternatives Rangkorrelationsmaß für Rangkorrelationen mit Rangbindungen ; )
Super Erklärung…. Vielen dank!
LG.
Judith
Großartig :)! Verständliche und trotzdem inhaltlich hochwertige Statistik-Seiten sind eine absolute Rarität! Danke für dein Engagement!!
und noch eine Frage, wann verwendet man Pearson und wann Spearman?
Dazu gibt es keine klare Regel. Oft macht es sogar Sinn, beide zu berechnen und zu sehen ob sie einigermaßen gleich, oder verschieden voneinander sind.
Übersehe ich etwas? Nach meinem derzeitigen Kenntnisstand ist das nicht egal; die Rangkorrelation nach Spearman hat doch im gegensatz zu Pearson den Vorteil, dass die Daten nicht normalverteilt sein müssen, und vor allem reicht ordinales Datennivau?
eine Frage dazu,
kann man die verkürzte Formel auch anwenden, wenn Ränge doppelt vorkommen?
Oder geht die vereinfachte Formel nur, wenn keine Ränge doppelt vorkommen?
Das habe ich vergessen zu erwähnen: Sie gilt nur wenn keine doppelten Ränge vorkommen. Ich habe den Artikel gerade mit dieser Bemerkung ergänzt. Danke für den Hinweis 🙂
– Alex
Hallo,
danke für die super Erklärung. Ich hatte mich vorher schon echt gequält das alte Wissen aufzufrischen. 🙂
Eine kleine Frage habe ich aber leider noch:
Muss/Sollte man das Ergebniss (bei meinen Daten 0,39) dann noch auf seine Signifikanz prüfen? Kannst du mir da vielleicht einen Stichpunkt nennen zum weiterforschen?
Nochmal vielen Dank!
Es gibt Signifikanztests für Korrelationen, ja. Der Absatz hier hilft vielleicht:
https://de.wikipedia.org/wiki/Korrelationskoeffizient#Signifikanzbedingung
Kleinen typo entdeckt:
In der Tabelle unter „Eine kürzere Formel für die Spearman-Korrelation“ steht
Person i Alter xi Rang des Alters rang(xi) Zeit in Sekunden yi Platzierung rang(xi) Rangdifferenz di=rang(xi)−rang(xi)
Hier hat sich ein x für ein y eingeschlichen. Es muss heißen:
Platzierung rang(yi), Rangdifferenz di=rang(xi)-rang(yi)
Ansonsten super.
gr, Tobias
Yes. Wahrscheinlich übermüdetes copy+paste 🙂
Vielen Dank, ist korrigiert!
Super Erklärung, vielen vielen Dank!!
VG Sercan
Vielen Dank für die ausführliche, verständliche Erklärung.
Echt starker Content hier!
Vielen vielen Dank für die super Erklarung! Das hat mir jetzt sehr viel geholfen! Endlich eine Seite, wo man alles verstandlich erklart bekommt!
LG
Sylvia