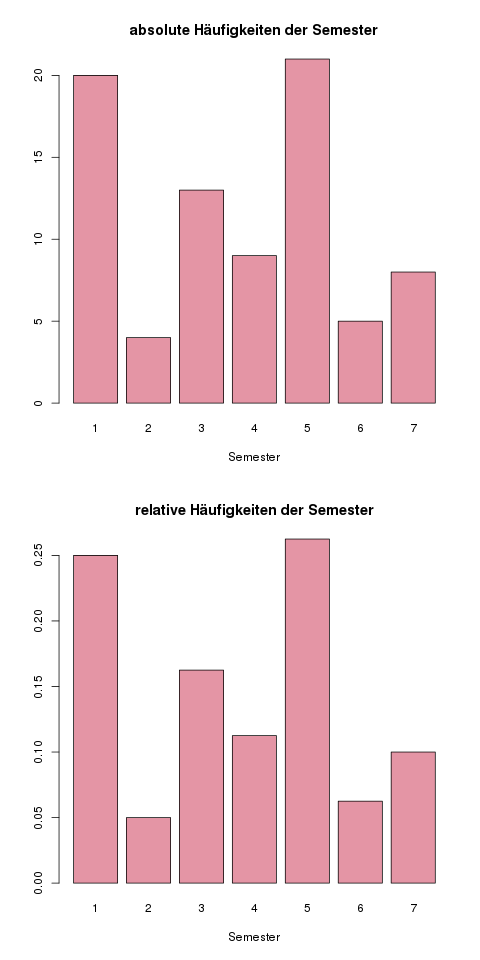
Streudiagramme (oft auch Scatterplots genannt) sind gleichzeitig eine der einfachsten und informativsten grafischen Darstellungen von Daten. Sie sind hauptsächlich für die gleichzeitige Darstellung von zwei Variablen geeignet.
Ein Beispiel ist der folgende Datensatz, in dem bei einer Reihe von Autos Vollbremsungen durchgeführt wurden, und die Ausgangsgeschwindigkeit (\(x\)-Achse) und der resultierende Bremsweg (\(y\)-Achse) gemessen wurde:
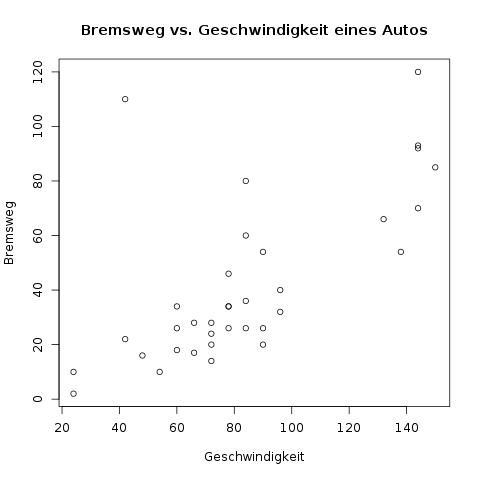 Durch die Darstellung der Daten fallen hier direkt drei Dinge auf:
Durch die Darstellung der Daten fallen hier direkt drei Dinge auf:
- Es wurden keine Autos gemessen, deren Geschwindigkeit zwischen 100 km/h und 130 km/h war. Das kann an der Studie liegen, oder es ist ein Fehler bei der Datenverarbeitung unterlaufen.
- Ein Auto hatte eine Ausgangsgeschwindigkeit von ca. 40 km/h, aber einen Bremsweg von 110 Metern. Das ist ein Ausreißer, für den nachgeforscht werden muss was da passiert ist. Hat der Fahrer geschlafen, oder vielleicht der, der die Messungen in den Computer eingegeben hat, einen Fehler gemacht?
- Der Zusammenhang wird hier besser durch eine Parabel als durch eine Gerade modelliert. Das macht Sinn, denn wenn man sich an die Fahrschule erinnert, ist der Bremsweg quadratisch abhängig von der Geschwindigkeit.
Eine grafische Darstellung und Exploration eines Datensatzes ist also immer ein sinnvoller erster Schritt, noch vor irgendwelchen statistischen Modellierungen.
Streudiagramme für drei Variablen sind möglich, aber meistens unübersichtlich. Als Beispiel wird hier ein Datensatz von verschiedenen Autos visualisiert, in dem drei Variablen (Gewicht, Hubraum, und Benzinverbrauch) dargestellt werden:
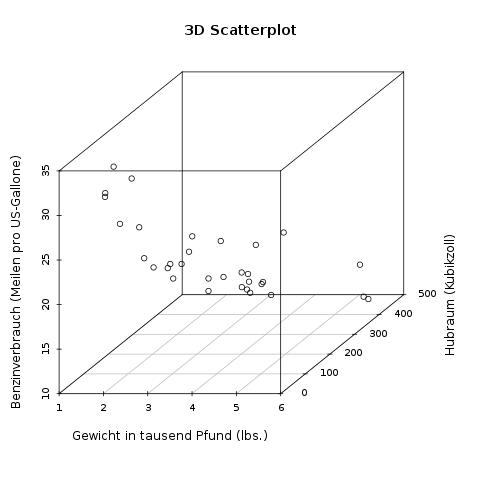 Wie gesagt, 3d-Streudiagramme sind nicht zu empfehlen, und wären auf dem Papier auch nur schwer zu zeichnen.
Wie gesagt, 3d-Streudiagramme sind nicht zu empfehlen, und wären auf dem Papier auch nur schwer zu zeichnen.
Zeichnen eines Streudiagramms
Um ein Streudiagramm zu zeichnen, benötigt man eine Reihe von gepaarten Messungen \(x_i\) und \(y_i\). Das können z.B. zwei Spalten, also zwei Variablen aus einem Datensatz sein, oder einfach die beiden gemessenen Merkmale in irgend einer Liste.
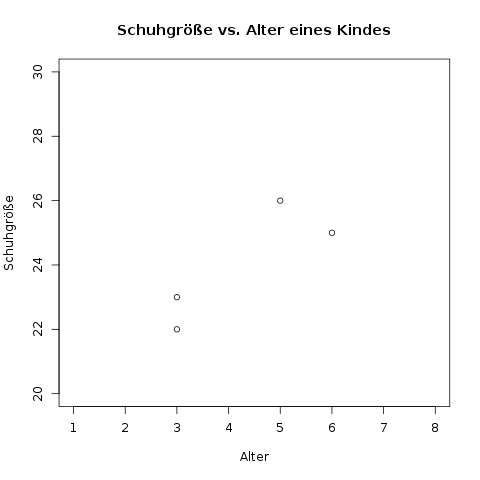
Als beispielhafte Daten schauen wir uns die Messungen \(x_i\) = Alter eines Kindes und \(y_i\) = Schugröße eines Kindes an. Wir bekommen die folgende Tabelle:
| Kind \(i\) | Alter \(x_i\) | Schuhgröße \(y_i\) |
|---|---|---|
| 1 | 3 | 22 |
| 2 | 5 | 26 |
| 3 | 3 | 23 |
| 4 | 6 | 25 |
Das erste Kind erhält nun einen Punkt der auf der \(x\)-Achse den Wert 3 hat, und auf der \(y\)-Achse den Wert 22. Genauso wird mit den übrigen drei Kindern verfahren. Das Streudiagramm für die 4 Kinder sieht wie folgt aus:

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!